Генератор чисел (ГЧ) на основе линейной конгруэнтной последовательности X
i+1 = ( AЧ Xi + B)(mod C), не обеспечивающий полного периода, когда C – простое число.
|
В статье описаны принципы получения чисел на основе |
Дегтяренко А. Ф. |
|
линейной конгруэнтной последовательности вида |
Областное государственное |
|
Xi+1 = (A Ч Xi + B)(mod C), в которой не обеспечивается полный |
предприятие электросвязи |
|
период генерации чисел в диапазоне от 0 до C – 1, и тем не менее, |
"Житомиртелеком”, т. 22-7755 |
|
количество рядов приближается к числу C!. C – простое число. |
E-mail: ztmtel@ukrpack.net |
_________________________________________________________________________________
__________Если рассматривать все тройки чисел A, B и C, входящих в выражение
Xi+1 = (AЧ Xi + B)(mod C), (1)
при условиях 0
Ј Xi < C, 1 < A< C, 0 < B < C, C > 3 и (A, C) = 1, (2)то все случаи, возникающие при этом, можно условно разделить на две части:
1. числа, обеспечивающие генерацию X
i в диапазоне 0 Ј Xi < C;2. числа, не обеспечивающие этого.
Первый случай достаточно полно теоретически и практически изложен в [1], и не является предметом рассмотрения в данной статье. В [1] также отмечено, что датчики случайных чисел этого типа были впервые предложены Д. Х. Лемером в 1948 г. Надо заметить, что количество троек 1-го случая гораздо меньше количества троек, которые относятся ко второму случаю. Второй случай также можно разделить на две части:
2.1 C – простое число, 2.2 C – составное число.
Сначала рассмотрим случай 2.1. Случай 2.2, когда C является произведением двух и более простых чисел, в том числе и некоторые вопросы для ГЧ с полным периодом, не затронутые в [1] – тема для другой статьи.
Далее в тексте статьи приняты следующие обозначения:
Т(n) – теоретико–числовая функция, численно равная количеству делителей числа n.
V(n) – функция Эйлера, численно равная количеству взаимно–простых чисел с n и не
превосходящих значения n. Согласно [2], функция V(n) от любого натурального
n>2 всегда чётная, т. е. V(n)
є 0 (mod 2); (3)![]() – i-тый множитель канонического разложения числа V(C), ci – его степень;
– i-тый множитель канонического разложения числа V(C), ci – его степень;
r – количество разных множителей числа С.
Далее нам понадобятся ссылки на теоремы, которые здесь приводятся без доказательств. Окончания теорем обозначены символом Ё .
Теорема BF. В линейной конгруэнтной последовательности (1), если
(А–1, С) = 1, то (4)
всегда существует, и при том единственное число X
i = Xa такое, чтоXa = (AЧ Xa + B)(mod C)Ё (5)
В случае, если С – простое число, условие (4) выполняется при любом A из (2).
Теорема BG. В выражении (1), если C – простое число, то весь диапазон чисел 0
ё (C–1) разбивается на m участков, каждый длиной s чисел, так чтоm · s = C – 1 = V(C) ; (6)
|
Если |
|
(7) |
то общее количество различных значений s равно ts:
ts = T(V(C)) – 1; (8)
Любое значение s не может быть чем–либо другим, кроме как делителем числа V(C), исключая 1.
ЁЭто значит, что наименьшее значение s = 2, или
1< s ЈV(C); (9)Количество участков при конкретном s равно m = V(C) / s; (10)
Теорема BL. Если в (1) А = С–1, то при любом С длина участка s минимальна и равна s = 2, а количество участков m максимально и равно m = (C–1)/2, если С нечетное, или m = C/2, если С – чётное.
ЁТеорема BN.
В выражении (1), при заданном простом числе C и выбранном значении s, обеспечивающим необходимое количество m участков, число A определяется из выражения: As = 1 (mod C); (11)Количество решений уравнения (11), (количество значений A, которые обеспечивают заданное количество участков при подстановке в выражение (1)), ta равно
ta = V(s); Ё (12)
При s = V(C) выражение (11) соответствует теореме Эйлера.
Таким образом, количество значений А, обеспечивающее максимальную длину участка s
max равно: tamax = V(V(C)). Естественно, что это количество значений А максимально. а количество участков при такой длине smax равно m = 1. Согласно теореме BL, минимальное количество значений А равно V(2) = 1. Поскольку общее количество значений А из диапазона (2) равно С – 2, то оставшееся количество значений А равно С – 3 – V(V(C)). И, наконец, общее количество значений А можно выразить формулой Гаусса [3]: С – 2 =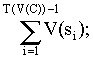 Здесь все значения si выбираются из выражения (8). Если предположить, что все значения А распределены равномерно между 1 и С–1, и если иметь в виду ограничение (14), то при С>4е+4, вышеупомянутые количества будут составлять » 0.99 и более от вычисленных.
Здесь все значения si выбираются из выражения (8). Если предположить, что все значения А распределены равномерно между 1 и С–1, и если иметь в виду ограничение (14), то при С>4е+4, вышеупомянутые количества будут составлять » 0.99 и более от вычисленных.
В ГЧ, имеющем полный период:
a) всегда, не зависимо от начального значения X[0], за конкретным значением Xa следует Xb, а за ним всегда следует конкретное значение Xc и т. д. Это нежелательное явление при использовании ГЧ в криптографии;
b) при проверке по всем тестам можно достичь отличных результатов, но невозможно сконструировать ГЧ, в периоде которого встречались бы “случайные неслучайности”;
c) увеличение количества чисел в таких ГЧ достигается только путём увеличения числа C. Если учесть, что обычная разрядность компьютера 232, то, чтобы не произошло переполнение разрядной сетки, необходимо выполнение условия:
(A·(C – 1)+B) Ј (232–1); (13)
A и B предпочтительно выбирать, согласно [1], из диапазонов:
C0.5 < A < (C – C0.5), (14)
ceil(k·C) Ј B Ј floor(k·C), (15)
где k = (![]()
floor – округление дробного числа путем отбрасывания дробной части;
ceil – тоже что floor, но с прибавлением к результату 1.
Подставляя в (13) из (14) и (15) сначала нижние границы диапазонов, а затем верхние, и решая его в целых числах относительно C, получим:
|
для нижней границы: |
A=1626, |
B=558128, |
C=2641089; |
|
для верхней границы: |
A=65408, |
B=13876, |
C=65665, |
Таким образом, используя 4-х байтную целую арифметику и ГЧ с полным периодом, можно получить ряд чисел максимальной длины
» 2.65 ·106. Использование же подпрограмм для 8–10-байтной арифметики существенно сказывается на скорости работы программы.В предлагаемом ГЧ с множеством участков (МГЧ) обычно количество участков m выбирается в пределах от 2 до 50. Если задать начальное значение X[0], принадлежащее i-му участку, то будут сгенерированы все значения X, принадлежащие этому участку и значения начнут повторяться. В этом случае необходимо взять X[0] с i+1-го участка, и так до тех пор, пока не
будут использованы X[0] со всех m участков. Таким образом, в итоге будут получены все C значений X в диапазоне от 0 до C – 1. Здесь учитывается и Xа, согласно теореме BF.Сгенерированный ряд чисел будет существенно зависеть от:
1.1 Порядка следования участков друг за другом. Количество вариантов следования участков друг за другом равно m! (m факториал);
1.2 Выбора начального значения X[0] с каждого участка. Количество сочетаний выбора начальных значений равно s
m;1.3 Способа выбора значений X на участках:
1.3.1 Последовательно, получив все значения X с i-го участка, как описано выше, перейти к участку i+1. И так переходить от участка к участку, пока не будет достигнут конец участка m;
1.3.2 Получив 1 (или n) значений с i-го участка, перейти к участку i+1, где также выбрать 1 (или n) значений. После участка m вновь вернутся на участок 1, и так по кругу двигаться до исчерпания всех значений на всех участках.
1.3.3 На участке i получить k значений, на участке j получить p значений. Иначе: номер очередного выбираемого участка – функция F1, количество выбираемых чисел с этого участка – функция F2. Переходя от участка к участку, получать разные количества X. При этом обеспечить равномерный закон распределения на протяжении от 0 до C – 1. Т. е., каждое число на участке от 0 до С – 1 должно встретиться только один раз.
1.3.4 Тоже, что в п. 1.3.3, но с соблюдением закона равномерного распределения на протяжении n·C. Т. е., каждое число из диапазона от 0 до С – 1 на протяжении n·C должно встретиться ровно n раз.
Всё это дaет возможность при заданных значениях A, B и C получить не 1 ряд сгенерированных чисел, как в случае полного периода, а приблизится к теоретически возможному количеству рядов: – C!. Используя только п. 1.3.1 и 1.3.2, можно получить m!· sm ; рядов, каждый длиной в С чисел. Для вышеописанного примера меньшее простое число C=2641061. Выбрав, скажем, m=43, находим s=61420, и количество чисел, которые можно получить при этом
N = 43! Ч 6142043Ч 2.641061Ч 106=1.25964Ч 10265.
На рис. 1 схематично представлен ГЧ с полным периодом генерации чисел,
на рис. 2 – МГЧ, при m = 5.
Описанный МГЧ используется совместно с многими другими элементами в разработанном автором криптографическом алгоритме, который условно назван SDK.
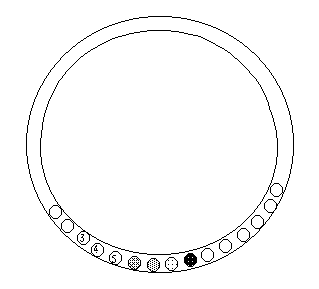
Рис. 1
.. 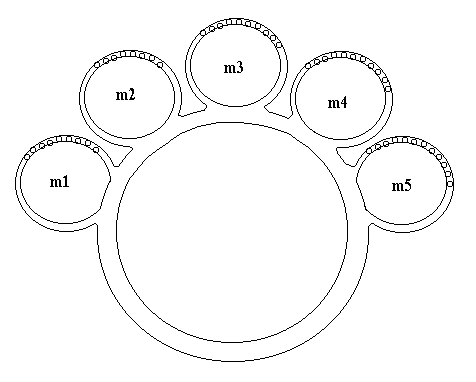
Рис. 2
Теперь более детально произведем разбор примера, в котором С – простое число. Предположим, что нам необходим МГЧ, в котором С находится в диапазоне 6·105 ± 5 % и m = 10 ± 2 . Подходящим простым числом является 582649. С – 1 = 582648 = 23·3·11·2207. Из этого видно, что количество участков может быть 2, 3, 4, 6, 8, 11, 12, 22 ... Наиболее подходит нам число m=11. Если бы в разложении С – 1 не было необходимого набора множителей – пришлось бы брать другое значение С. Далее: s = 582648 / 11 = 52968; Из (11), с учетом (13), (14) и (15) определяем A и B. Результаты расчетов для этого примера, а также для трёх других примеров, в которых C – простое число, сведены в таблицу 1.
Таблица 1
|
Пример 1 |
Пример 2 |
Пример 3 |
Пример 4 |
|
|
A = 7322 |
A = 7344 |
A = 7235 |
A = 7323 |
|
|
B = 122938 |
B = 122939 |
B = 123117 |
В = 123118 |
|
|
C = 582649 |
C = 583493 |
|||
|
m = 11 |
m = 12 |
m = 13 |
m = 14 |
|
|
s =52968 |
s =48554 |
s = 44884 |
s = 41678 |
|
|
Xa= 485876 |
Xa = 411797 |
Xa = 567586 |
Xa = 495498 |
|
|
X[0]i |
X[0]i |
X[0]i |
X[0]i |
|
|
26006 |
26010 |
26006 |
26010 |
|
|
26010 |
26012 |
26017 |
26014 |
|
|
26019 |
26032 |
26018 |
26018 |
|
|
26031 |
26035 |
26031 |
26032 |
|
|
26035 |
26040 |
26037 |
26040 |
|
|
26039 |
26046 |
26039 |
26041 |
|
|
26059 |
26062 |
26042 |
26045 |
|
|
26065 |
26072 |
26057 |
26047 |
|
|
26081 |
26077 |
26064 |
26049 |
|
|
26096 |
26083 |
26075 |
26060 |
|
|
26098 |
26084 |
26082 |
26076 |
|
|
|
26088 |
26088 |
26086 |
|
|
|
|
26098 |
26087 |
|
|
|
|
|
26099 |
|
Для приведенных четырех примеров были проведены статистические испытания
.Для каждого примера генерировались 4 файлa, согласно пунктов 1.3.1,
ё 1.3.4. Последние два файла генерировались длиной 3·C . Каждое значение X приводилось к диапазону 0 ё 1 и умножалось на 256. Полученные файлы проверялись статистическими тестами при уровне значимости 0.99 . Результаты тестирования приведены в таблице 2.Таблица 2.
|
Примеры |
Т е с т ы |
||||
|
№ и пункты |
Хи-квадрат |
Уолша |
серий |
инверсий |
|
|
1 п. 1.3.1 |
0.0034 |
1.08 |
2.51 |
1.85 |
|
|
п. 1.3.2 |
0.0034 |
1.71 |
3.06 |
2.20 |
|
|
п. 1.3.3 |
0.0102 |
1.12 |
2.59 |
2.00 |
|
|
п. 1.3.4 |
0.0102 |
1.19 |
2.41 |
2.24 |
|
|
2 п. 1.3.1 |
0.0034 |
1.23 |
2.03 |
2.13 |
|
|
п. 1.3.2 |
0.0034 |
1.41 |
3.23 |
2.15 |
|
|
п. 1.3.3 |
0.0102 |
1.18 |
2.30 |
2.01 |
|
|
п. 1.3.4 |
0.0102 |
1.21 |
2.52 |
2.05 |
|
|
3 п. 1.3.1 |
0.0228 |
1.38 |
2.74 |
1.85 |
|
|
п. 1.3.2 |
0.0228 |
1.38 |
4.18 |
2.25 |
|
|
п. 1.3.3 |
0.0684 |
1.33 |
2.62 |
1.94 |
|
|
п. 1.3.4 |
0.0684 |
1.36 |
2.14 |
1.92 |
|
|
4 п. 1.3.1 |
0.0228 |
1.12 |
2.43 |
1.70 |
|
|
п. 1.3.2 |
0.0228 |
1.67 |
5.18 |
2.37 |
|
|
п. 1.3.3 |
0.0684 |
1.26 |
2.50 |
1.94 |
|
|
п. 1.3.4 |
0.0684 |
1.36 |
2.25 |
1.95 |
|
В заключение приведу еще несколько теорем, которые касаются простых чисел. Идеи, вытекающие из этих теорем, прямо или косвенно затрагиваются в алгоритме SDK.
Теорема BQ. Если С – простое число, (С>3), то
(С – 2)!(mod C) = 1 и (С – 3)!(mod C) = (С–1)/2.
Ё (16)Теорема BR.
Если С – простое число, (C>3), и если С!+ – произведение четных чисел, до числа С, а С!– – произведение нечетных чисел до числа (С – 2), то:1. Если С(mod 4) = 1, то C!
– є C!+(mod C); (17)2. Если C(mod 4) = 3, то: либо С!
–(mod C) = 1 и C!+(mod C) = С–1, (18)либо наоборот, С!
+(mod C) = 1, а C!- (mod C) = С–1. ЁНа эту теорему очень похожа теорема BS.
Теорема BS. Если С – простое число, (C>3), и если С!
H – произведение чисел от 2 до (С–1)/2, а С!K – произведение чисел от (С–1)/2+1 до (С–1), то:1. Если С(mod 4) = 1, то C!
H є C!K(mod C); (19)2. Если C(mod 4) = 3, то: либо С!
H(mod C) = 1 и C!K(mod C) = С–1, (20)либо наоборот, С!К(mod C) = 1, а C!Н(mod C) = С–1.
ЁТеорема BU.
Если С – простое число, (C>3), то: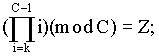 (21)
(21)
где Z = ((C–k)!)(mod C), если k(mod 2) = 1, иначе
Z = C–((C–k)!)(mod C), если k(mod 2) = 0.
ЁТеорема BV.
Число С является простым тогда и только тогда, когда не существует таких натуральных чисел X > 0 и Y > 0, которые удовлетворяют равенствуС – 1 = X + Y + XY; (22)
Справедливо и обратное утверждение: если существуют натуральные числа X >0 и Y > 0, такие, что подстановка их в выражение (22) превращает его в тождество, то С – составное число. Ё
Этот факт можно использовать как еще одно "решето" для определения простых чисел. Обозначив C – 1 = K, а X + 1 = K1, (23)
При X = Y, определим корни уравнения X
2 + 2Ч X – K = 0. (24)Получим X1= sqrt(C)–1; что только на 1 меньше, чем в решете Эратосфена. Теперь теорему BV можно перефразировать следующим образом:
Число С является простым тогда и только тогда, когда
K (mod K1) № X (25)
при всех Х в диапазоне от 2
Ј X Ј X1 и X(mod 2) є 0. ЁЕстественно, что теорему BV можно использовать не только для нахождения простых чисел, а и для разложения составных чисел на множители. Из этого можно сделать вывод, что это решето не имеет сколь–нибудь заметных преимуществ перед решетом Эратосфена. Но в некоторых случаях, когда нужны числа X и Y из (22), удобнее пользоваться этим решетом, ибо, согласно следующей теореме BW, в этом случае существует хотя бы одна пара таких чисел.
Теорема BW. Если в выражении (22) С – составное число, то t — количество различных пар значений X и Y всегда существует и определяется выражением:
t = (T(C) + T(C)(mod 2) – 2)/2. (26)
Если T(C)(mod 2)
№ 0, то среди всех X, Y одна пара такая, что X = Y; ЁИз этой теоремы непосредственно вытекает
Теорема BY. Если T(C)(mod 2)
№ 0, то sqrt(C) = K1, (27)где K1 – натуральное число, причем K1 = X + 1 из (22).
Ё
ЛИТЕРАТУРА
1. Кнут Д. Искусство программирования для ЭВМ: пер. с англ.– М.: Мир, 1977.– Т.2.
2. Бородiн О. А. Теорiя чисел. –Киев: Радянська школа, 1965. – С. 81.
3. Сушкевич А. К. Теория чисел. Элементарный курс. – Харьков. Изд. Харьковского университе-
та. – 1954. – С. 65.