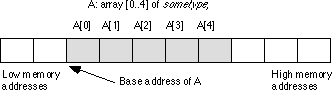
y is also a valid index, with x < y, then all i
such that x < i < y are valid indices into the array.A[i] chooses
the ith element from array A. Note that
there is no formal requirement that element i be anywhere near
element i+1 in memory. As long as A[i] always
refers to the same memory location and A[i+1] always refers
to its corresponding location (and the two are different), the definition
of an array is satisfied.
The base address of an array is the address of the first element on the
array and always appears in the lowest memory location. The second array
element directly follows the first in memory, the third element follows
the second, etc. Note that there is no requirement that the indices start
at zero. They may start with any number as long as they are contiguous.
However, for the purposes of discussion, it's easier to discuss accessing
array elements if the first index is zero. This text generally begins most
arrays at index zero unless there is a good reason to do otherwise. However,
this is for consistency only. There is no efficiency benefit one way or
another to starting the array index at some value other than zero.
To access an element of an array, you need a function that converts an array
index into the address of the indexed element. For a single dimension array,
this function is very simple. It is
Element_Address = Base_Address + ((Index - Initial_Index) * Element_Size)where
Initial_Index is the value of the first index in the
array (which you can ignore if zero) and the value Element_Size
is the size, in bytes, of an individual element of the array.arrayname basetype n dup (?)Arrayname is the name of the array variable and basetype is the type of an element of that array. This sets aside storage for the array. To obtain the base address of the array, just use arrayname.
n dup (?) operand tells the assembler to duplicate the
object inside the parentheses n times. Since a question mark appears inside
the parentheses, the definition above would create n occurrences of an uninitialized
value. Now let's look at some specific examples:
CharArray char 128 dup (?) ;array[0..127] of char IntArray integer 8 dup (?) ;array[0..7] of integer BytArray byte 10 dup (?) ;array[0..9] of byte PtrArray dword 4 dup (?) ;array[0..3] of dwordThe first two examples, of course, assume that you've used the
typedef
statement to define the char and integer data
types.RealArray real4 8 dup (1.0) IntegerAry integer 8 dup (1)These definitions both create arrays with eight elements. The first definition initializes each four-byte real value to 1.0, the second declaration initializes each integer element to one.
name type value1, value2, value3, ..., valuenThis form allocates n variables of type type. It initializes the first item to value1, the second item to value2, etc. So by simply enumerating each value in the operand field, you can create an array with the desired initial values. In the following integer array, for example, each element contains the square of its index:
Squares integer 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100If your array has more elements than will fit on one line, there are several ways to continue the array onto the next line. The most straight-forward method is to use another integer statement but without a label:
Squares integer 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
integer 121, 144, 169, 196, 225, 256, 289, 324
integer 361, 400
Another option, that is better in some circumstances, is to use a backslash
at the end of each line to tell MASM 6.x to continue reading data on the
next line:
Squares integer 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, \
121, 144, 169, 196, 225, 256, 289, 324, \
361, 400
Of course, if your array has several thousand elements in it, typing them
all in will not be very much fun. Most arrays initialized this way have
no more than a couple hundred entries, and generally far less than 100.BigArray word 256 dup (0,1,2,3)This array has 1024 elements, not 256. The
n dup (xxxx) operand
tells MASM to duplicate xxxx n times, not create an array with
n elements. If xxxx consists of a single item, then the dup
operator will create an n element array. However, if xxxx contains
two items separated by a comma, the dup operator will create
an array with 2*n elements. If xxxx contains three items separated
by commas, the dup operator creates an array with 3*n items,
and so on. Since there are four items in the parentheses above, the dup
operator creates 256*4 or 1024 items in the array. The values in the array
will initially be 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 ...dup operator
when looking at multidimensional arrays a little later.Base_Address entry you can use the name of the array
(since MASM associates the address of the first operand with the label).
The Element_Size entry is the number of bytes for each array
element. If the object is an array of bytes, the Element_Size
field is one (resulting in a very simple computation). If each element of
the array is a word (or integer, or other two-byte type) then Element_Size
is two. And so on. To access an element of the Squares
array in the previous section, you'd use the formula:AX:=Squares[index]
is
mov bx, index
add bx, bx ;Sneaky way to compute 2*bx
mov ax, Squares [bx]
There are two important things to notice here. First of all, this code uses
the add instruction rather than the mul instruction
to compute 2*index. The main reason for choosing add is that
it was more convenient (remember, mul doesn't work with constants
and it only operates on the ax register). It turns out that
add is a lot faster than mul on many processors,
but since you probably didn't know that, it wasn't an overriding consideration
in the choice of this instruction.mov ax, Squares[bx] loads ax
from location Squares+bx which is the base address plus index*2
(since bx contains index*2). Sure, you could have used
lea ax, Squares
add bx, ax
mov ax, [bx]
in place of the last instruction, but why use three instructions where one
will do the same job? This is a good example of why you should know your
addressing modes inside and out. Choosing the proper addressing mode can
reduce the size of your program, thereby speeding it up.
mov ebx, index ;Assume a 32 bit value.
mov ax, Squares [ebx*2]
This brings the instruction count down to two instructions. You'll soon
see that two instructions aren't necessarily faster than three instructions,
but hopefully you get the idea. Knowing your addressing modes can surely
help.Squares
array. However, if you access several different elements from the array
within a short section of code, and you can afford to dedicate another register
to the operation, you can certainly shorten your code and, perhaps, speed
it up as well. The mov ax,Squares[BX] instruction is four bytes
long (assuming you need a two-byte displacement to hold the offset to Squares
in the data segment). You can reduce this to a two byte instruction by using
the base/indexed addressing mode as follows:
lea bx, Squares
mov si, index
add si, si
mov ax, [bx][si]
Now bx contains the base address and si contains
the index*2 value. Of course, this just replaced a single four-byte instruction
with a three-byte and a two-byte instruction, hardly a good trade-off. However,
you do not have to reload bx with the base address of Squares
for the next access. The following sequence is one byte shorter than the
comparable sequence that doesn't load the base address into bx:
lea bx, Squares
mov si, index
add si, si
mov ax, [bx][si]
.
. ;Assumption: BX is left alone
. ; through this code.
mov si, index2
add si, si
mov cx, [bx][si]
Of course the more accesses to Squares you make without reloading
bx, the greater your savings will be. Tricky little code sequences
such as this one sometimes pay off handsomely. However, the savings depend
entirely on which processor you're using. Code sequences that run faster
on an 8086 might actually run slower on an 80486 (and vice versa). Unfortunately,
if speed is what you're after there are no hard and fast rules. In fact,
it is very difficult to predict the speed of most instructions on the simple
8086, even more so on processors like the 80486 and Pentium/80586 that offer
pipelining, on-chip caches, and even superscalar operation. A:array[0..3,0..3]
of char. This array contains 16 bytes organized as four rows of four
characters. Somehow you've got to draw a correspondence with each of the
16 bytes in this array and 16 contiguous bytes in main memory. The figure
below shows one way to do this.
The actual mapping is not important as long as two things occur: (1)
each element maps to a unique memory location (that is, no two entries in
the array occupy the same memory locations) and (2) the mapping is consistent.
That is, a given element in the array always maps to the same memory location.
So what you really need is a function with two input parameters (row and
column) that produces an offset into a linear array of sixteen bytes.
Now any function that satisfies the above constraints will work fine. Indeed,
you could randomly choose a mapping as long as it was unique. However, what
you really want is a mapping that is efficient to compute at run time and
works for any size array (not just 4x4 or even limited to two dimensions).
While there are a large number of possible functions that fit this bill,
there are two functions in particular that most programmers and most high
level languages use: row major ordering and column major ordering.
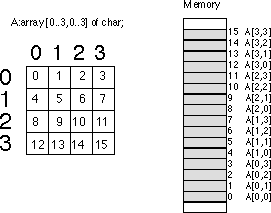
Row major ordering is the method employed by most high level programming
languages including Pascal, C, Ada, Modula-2, etc. It is very easy to implement
and easy to use in machine language (especially within a debugger such as
CodeView). The conversion from a two-dimensional structure to a linear array
is very intuitive. You start with the first row (row number zero) and then
concatenate the second row to its end. You then concatenate the third row
to the end of the list, then the fourth row, etc:

For those who like to think in terms of program code, the following nested Pascal loop also demonstrates how row major ordering works:
index := 0;
for colindex := 0 to 3 do
for rowindex := 0 to 3 do
begin
memory [index] := rowmajor [colindex][rowindex];
index := index + 1;
end;
The important thing to note from this code, that applies across the board
to row major order no matter how many dimensions it has, is that the rightmost
index increases the fastest. That is, as you allocate successive memory
locations you increment the rightmost index until you reach the end of the
current row. Upon reaching the end, you reset the index back to the beginning
of the row and increment the next successive index by one (that is, move
down to the next row.). This works equally well for any number of dimensions.
The following Pascal segment demonstrates row major organization for a 4x4x4
array:
index := 0;
for depthindex := 0 to 3 do
for colindex := 0 to 3 do
for rowindex := 0 to 3 do begin
memory [index] := rowmajor [depthindex][colindex][rowindex];
index := index + 1;
end;
The actual function that converts a list of index values into an offset
doesn't involve loops or much in the way of fancy computations. Indeed,
it's a slight modification of the formula for computing the address of an
element of a single dimension array. The formula to compute the offset for
a two-dimension row major ordered array declared as A:array [0..3,0..3]
of integer is
Element_Address = Base_Address + (colindex * row_size + rowindex) * Element_SizeAs usual,
Base_Address is the address of the first element
of the array (A[0][0] in this case) and Element_Size
is the size of an individual element of the array, in bytes. Colindex
is the leftmost index, rowindex is the rightmost index into
the array. Row_size is the number of elements in one row of
the array (four, in this case, since each row has four elements). Assuming
Element_Size is one, This formula computes the following offsets
from the base address:
Column Index Row Index Offset into Array
0 0 0
0 1 1
0 2 2
0 3 3
1 0 4
1 1 5
1 2 6
1 3 7
2 0 8
2 1 9
2 2 10
2 3 11
3 0 12
3 1 13
3 2 14
3 3 15
For a three-dimensional array, the formula to compute the offset into memory
is the following:
Address = Base + ((depthindex*col_size+colindex) * row_size + rowindex) * Element_Size
Col_size is the number of items in a column, row_size
is the number of items in a row. In Pascal, if you've declared the array
as "A:array [i..j] [k..l] [m..n] of type;" then row_size
is equal to n-m+1 and col_size is equal to l-k+1.A:array [g..h] [i..j]
[k..l] [m..n] of type;" the formula for computing the address
of an array element is
Address = Base + (((LeftIndex * depth_size + depthindex)*col_size+colindex) * row_size + rowindex) * Element_Size
Depth_size is equal to i-j+1, col_size and
row_size are the same as before. LeftIndex represents
the value of the leftmost index.A: array [0..3] of sometype;Assume that sometype is the type "
sometype = array [0..3] of
char;".A is a single dimension array. Its individual elements happen
to be arrays, but you can safely ignore that for the time being. The formula
to compute the address of an element of a single dimension array is
Element_Address = Base + Index * Element_SizeIn this case
Element_Size happens to be four since each element
of A is an array of four characters. So what does this formula
compute? It computes the base address of each row in this 4x4 array of characters:
Of course, once you compute the base address of a row, you can reapply
the single dimension formula to get the address of a particular element.
While this doesn't affect the computation at all, conceptually it's probably
a little easier to deal with several single dimension computations rather
than a complex multidimensional array element address computation.
Consider a Pascal array defined as "A:array [0..3] [0..3] [0..3]
[0..3] [0..3] of char;" You can view this five-dimension array
as a single dimension array of arrays:
type
OneD = array [0..3] of char;
TwoD = array [0..3] of OneD;
ThreeD = array [0..3] of TwoD;
FourD = array [0..3] of ThreeD;
var
A : array [0..3] of FourD;
The size of OneD is four bytes. Since TwoD contains
four OneD arrays, its size is 16 bytes. Likewise, ThreeD
is four TwoDs, so it is 64 bytes long. Finally, FourD
is four ThreeDs, so it is 256 bytes long. To compute the address
of "A [b] [c] [d] [e] [f]" you could use the following
steps:
for i := 0 to 4 do base := base + A1[i] * A2[i];Presumably
base contains the base address of the array before
executing this loop. Note that you can easily extend this code to any number
of dimensions by simply initializing A1 and A2
appropriately and changing the ending value of the for loop.A
[b,c,d,e,f]" into a Pascal program, not realizing what the compiler
is doing with the code. Assembly language programmers are not so cavalier
- they see the mess you wind up with when you use higher dimension arrays.
Indeed, good assembly language programmers try to avoid two dimension arrays
and often resort to tricks in order to access data in such an array when
its use becomes absolutely mandatory. But more on that a little later.
The formulae for computing the address of an array element when using
column major ordering is very similar to that for row major ordering. You
simply reverse the indexes and sizes in the computation:
For a two-dimension column major array:
Element_Address = Base_Address + (rowindex * col_size + colindex) * Element_SizeFor a three-dimension column major array:
Address = Base + ((rowindex*col_size+colindex) * depth_size + depthindex) * Element_SizeFor a four-dimension column major array:
Address = Base + (((rowindex * col_size + colindex)*depth_size+depthindex) * Left_size + Leftindex) * Element_SizeThe single Pascal loop provided for row major access remains unchanged (to access
A [b] [c] [d] [e] [f]):
for i := 0 to 4 do base := base + A1[i] * A2[i];Likewise, the initial values of the A1 array remain unchanged:
A1 = {256, 64, 16, 4, 1}
The only thing that needs to change is the initial values for the A2 array,
and all you have to do here is reverse the order of the indices:
A2 = {f, e, d, c, b}
dup operator for reserving storage. n
dup (xxxx) replicates xxxx n times. As you saw earlier,
this dup operator allows not just one, but several items within
the parentheses and it duplicates everything inside the specified number
of times. In fact, the dup operator allows anything that you
might normally expect to find in the operand field of a byte
statement including additional occurrences of the DUP operator.
Consider the following statement:
A byte 4 dup (4 dup (?))The first
dup operator repeats everything inside the parentheses
four times. Inside the parentheses the 4 DUP (?) operation
tells MASM to set aside storage for four bytes. Four copies of four bytes
yields 16 bytes, the number necessary for a 4 x 4 array. Of course, to reserve
storage for this array you could have just as easily used the statement:
A byte 16 dup (?)Either way the assembler is going to set aside 16 contiguous bytes in memory. As far as the 80x86 is concerned, there is no difference between these two forms. On the other hand, the former version provides a better indication that
A is a 4 x 4 array than the latter version. The latter
version looks like a single dimension array with 16 elements.A:array [0..2, 0..3,
0..4] of integer might be
A integer 3 dup (4 dup (5 dup (?)))(of course, you will need the
integer typedef word statement
in your program for this to work.)A integer 3 dup (4 dup (5 dup (1)))If you want to initialize each element of the array to a different value, you'll have to enter each value individually. If the size of a row is small enough, the best way to approach this task is to place the data for each row of an array on its own line. Consider the following 4x4 array declaration:
A integer 0,1,2,3
integer 1,0,1,1
integer 5,7,2,2
integer 0,0,7,6
Once again, the assembler doesn't care where you split the lines, but the
above is much easier to identify as a 4x4 array than the following that
emits the exact same data:
A integer 0,1,2,3,1,0,1,1,5,7,2,2,0,0,7,6Of course, if you have a large array, an array with really large rows, or an array with many dimensions, there is little hope for winding up with something reasonable. That's when comments that carefully explain everything come in handy.
mov, add, and mul instructions make short
work of the various equations that compute offsets into multidimensional
arrays. Let's consider a two dimension array first:
; Note: TwoD's row size is 16 bytes.
TwoD integer 4 dup (8 dup (?))
i integer ?
j integer ?
. .
. .
. .
; To peform the operation TwoD[i,j] := 5; you'd use the code:
mov ax, 8 ;8 elements per row
mul i
add ax, j
add ax, ax ;Multiply by element size (2)
mov bx, ax ;Put in a register we can use
mov TwoD [bx], 5
Of course, if you have an 80386 chip (or better), you could use the following
code:
mov eax, 8 ;Zeros H.O. 16 bits of EAX.
mul i
add ax, j
mov TwoD[eax*2], 5
Note that this code does not require the use of a two register addressing
mode on the 80x86. Although an addressing mode like TwoD [bx][si]
looks like it should be a natural for accessing two dimensional arrays,
that isn't the purpose of this addressing mode.
ThreeD integer 4 dup (4 dup (4 dup (?)))
i integer ?
j integer ?
k integer ?
. .
. .
. .
; To peform the operation ThreeD[i,j,k] := 1; you'd use the code:
mov bx, 4 ;4 elements per column
mov ax, i
mul bx
add ax, j
mul bx ;4 elements per row
add ax, k
add ax, ax ;Multiply by element size (2)
mov bx, ax ;Put in a register we can use
mov ThreeD [bx], 1
Of course, if you have an 80386 or better processor, this can be improved
somewhat by using the following code:
mov ebx, 4
mov eax, ebx
mul i
add ax, j
mul bx
add k
mov ThreeD[eax*2], 1