By convention, we'll always assume that the starting state is state zero.
We will denote final states (there may be more than one) by using a double
circle for the state (state eight is the final state above).
An NFA always begins with an input string in the starting state (state zero).
On each edge coming out of a state there is either 
, a single character,
or a character string. To help unclutter the NFA diagrams, we will allow
expressions of the form " xxx | yyy | zzz | " where xxx, yyy,
and zzz are , a single character, or a character string. This corresponds
to multiple edges from one state to the other with a single item on each
edge. In the example above,
is equivalent to
Likewise, we will allow sets of characters, specified by a string of
the form x-y, to denote the expression x | x+1 | x+2 | ... | y.
Note that an NFA accepts a string if there is some path from the starting
state to an accepting state that exhausts the input string. There may be
multiple paths from the starting state to various final states. Furthermore,
there may be some particular path from the starting state to a non-accepting
state that exhausts the input string. This does not necessarily mean the
NFA rejects that string; if there is some other path from the starting state
to an accepting state, then the NFA accepts the string. An NFA rejects a
string only if there are no paths from the starting state to an accepting
state that exhaust the string.
Passing through an accepting state does not cause the NFA to accept a string.
You must wind up in a final state and exhaust the input string.
To process an input string with an NFA, begin at the starting state. The
edges leading out of the starting state will have a character, a string,
or associated with them. If you choose to move from one state
to another along an edge with a single character, then remove that character
from the input string and move to the new state along the edge traversed
by that character. Likewise, if you choose to move along an edge with a
character string, remove that character string from the input string and
switch to the new state. If there is an edge with the empty string, ,
then you may elect to move to the new state given by that edge without removing
any characters from the input string.
Consider the string "1.25e2" and the NFA in Figure 16.1. From
the starting state we can move to state one using the string (there is
no leading plus or minus, so is our only option). From state one
we can move to state two by matching the "1" in our input string
with the set 0-9; this eats the "1" in our input string leaving
".25e2". In state two we move to state three and eat the period
from the input string, leaving "25e2". State three loops on itself
with numeric input characters, so we eat the "2" and "5"
characters at the beginning of our input string and wind up back in state
three with a new input string of "e2". The next input character
is "e", but there is no edge coming out of state three with an
"e" on it; there is, however, an -edge, so we can
use that to move to state four. This move does not change the input string.
In state four we can move to state five on an "e" character. This
eats the "e" and leaves us with an input string of "2".
Since this is not a plus or minus character, we have to move from state
five to state six on the edge. Movement from state six to state
seven eats the last character in our string. Since the string is empty (and,
in particular, it does not contain any digits), state seven cannot loop
back on itself. We are currently in state seven (which is not a final state)
and our input string is exhausted. However, we can move to state eight (the
accepting state) since the transition between states seven and eight is
an edge. Since we are in a final state and we've exhausted
the input string, This NFA accepts the input string.
(the empty set) is a single, non-accepting state.
, a single character,
or a string, create two states and draw an arc between them with ,
the single character, or the string as the label. For example, the RE "a"
is converted to an NFA as
The following example converts the regular expression for an integer
constant to an NFA. The first step is to create an NFA for the regular expression
(+ | - | ). The complete construction becomes
Although we can obviously optimize this to
The next step is to handle the [0-9]+ regular expression; after some minor optimization, this becomes the NFA
Now we simply concatenate the results to produce:
All we need now are starting and final states. The starting state is
always the first state of the NFA created by the conversion of the leftmost
item in the regular expression. The final state is always the last state
of the NFA created by the conversion of the rightmost item in the regular
expression. Therefore, the complete regular expression for integer constants
(after optimizing out the middle edge above, which serves no purpose) is
AltRST proc near
push ax ;The purpose of these two instructions
mov ax, di ; is to preserve di in case of failure.
call r
jc Success
mov di, ax ;Restore di (it may be modified by r).
call s
jc Success
mov di, ax ;Restore di (it may be modified by s).
call t
Success: pop ax ;Restore ax.
ret
AltRST endp
If the r matching procedure succeeds, there is no need to try
s and t. On the other hand, if r
fails, then we need to try s. Likewise, if r and
s both fail, we need to try t. AltRST
will fail only if r, s, and t all
fail. This code assumes that es:di points at the input string
to match. On return, es:di points at the next available character
in the string after a match or it points at some arbitrary point if the
match fails. This code assumes that r, s, and
t all preserve the ax register, so it preserves
a pointer to the current point in the input string in ax in
the event r or s fail.or a single character) is not hard at all. Suppose the
matching function r matches the regular expression (+ | - | ). The complete
procedure for r is
r proc near
cmp byte ptr es:[di], '+'
je r_matched
cmp byte ptr es:[di], '-'
jne r_nomatch
r_matched: inc di
r_nomatch: stc
ret
r endp
Note that there is no explicit test for .
If is one of the alternatives,
the function attempts to match one of the other alternatives first. If none
of the other alternatives succeed, then the matching function will succeed
anyway, although it does not consume any input characters (which is why
the above code skips over the inc di instruction if it does
not match "+" or "-"). Therefore, any matching function
that has as an alternative will always succeed. s matching function accepts a single decimal digit. the code
for s might be the following:
s proc near
cmp byte ptr es:[di], '0'
jb s_fails
cmp byte ptr es:[di], '9'
ja s_fails
inc di
stc
ret
s_fails: clc
ret
s endp
If an NFA takes the form:
Where x is any arbitrary character or string or ,
the corresponding assembly code for this procedure would be
ConcatRxS proc near
call r
jnc CRxS_Fail ;If no r, we won't succeed
; Note, if x=e then simply delete the following three statements.
; If x is a string rather than a single character, put the the additional
; code to match all the characters in the string.
cmp byte ptr es:[di], 'x'
jne CRxS_Fail
inc di
call s
jnc CRxS_Fail
stc ;Success!
ret
CRxS_Fail: clc
ret
ConcatRxS endp
If the regular expression is of the form r* and the corresponding NFA is
of the form
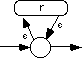
Then the corresponding 80x86 assembly code can look something like the
following:
RStar proc near
call r
jc RStar
stc
ret
RStar endp
Regular expressions based on the Kleene star always succeed since they allow
zero or more occurrences. That is why this code always returns with the
carry flag set.
RPlus proc near
call r
jnc RPlus_Fail
RPlusLp: call r
jc RPlusLp
stc
ret
RPlus_Fail: clc
ret
RPlus endp
Note how this routine fails if there isn't at least one occurrence of r.