5.1.2. Near-Field Dosimetry

blue line

The methods used to calculate near-field SARs are similar to those used to calculate planewave SARs. Since the basic methods were described in Section 5.1.1, the comments here are directed mostly toward the differences required in using the techniques in near-field analyses.

Long-Wavelength Approximation--The long-wavelength approximation used for planewave calculations has been useful for some near-field calculations in spheroids. In the approximation for near fields, the incident near field is averaged along the major axis of the spheroid; the SARs calculated this way are surprisingly close to those calculated by more accurate methods. The advantage of the long-wavelength approximation is its relative simplicity.

Extended-Boundary-Condition Method-By expanding the incident near fields in spherical harmonics, we have been able to use the EBCM for calculating near-field SARs. Since these calculations are more complex than those for planewaves, the EBCM may not be useful up to 80 MHz for near-field calculations, as it is for planewave calculations.

Iterative-Extended-Boundary-Condition Method--Expanding the incident near fields in spherical harmonics allows use of the IEBCM, which greatly extends the range of calculations possible with the EBCM, just as for planewave calculations.

Cylindrical Approximation--in planewave dosimetry, the SAR calculated for a cylinder was a good approximation to that calculated for a spheroid in the frequency range where the wavelength was short compared to the length of the spheroid. Similarly, the same approximation was valid for near-field calculations and was used in calculating SARs at frequencies above resonance for data in this report. In fact, for sources very close to an absorber, the cylindrical approximation is even better for near fields than for far fields. For the cylindrical models SAR calculations were made by the classical eigenfunction expansion method.

Planewave Spectrum Method--Chatterjee et al. (1980a, 1980b, 1980c, 1982b) expressed incident near fields in terms of a spectrum of planewaves and then used the moment method to calculate local and average SARs in a block model of man. Some of their data are summarized in Chapter 6.

5.1.3. Sensitivity of SAR Calculations to Permittivity Changes

Since there is some variability in the permittivity of people and other animals and some uncertainty in the measurement of permittivity of tissue equivalent materials, knowing something about SAR sensitivity to permittivity changes is important. Figure 5.7 shows calculated average SAR as a function of frequency for several permittivity values in a prolate spheroidal model of an average man. For this case the SAR is not extremely sensitive to changes in permittivity. This appears to be generally true.

5.1.4. Relative Absorption Cross Section

Although commonly used in electromagnetics, particularly in describing the properties of objects detected by radar, the concepts of absorption cross section and scattering cross section apparently have not been used much by the bioelectromagnetics community. The basic concept of absorption cross section is explained here, and some examples of relative absorption cross sections are given.

The term "absorption cross section" (AC) is defined as the ratio of the total power absorbed by a target exposed to EM radiation to the incident-power density. The AC has the dimension of area and can be expressed in terms of the average SAR as

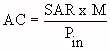equation (Equation 5.25)

where Pin is the incident power density and M is the mass of the object exposed to EM fields.

Figure 5.7.
Calculated average SAR in a prolate spheroidal model of an average man, as a function of frequency for several values of permittivity. epsilonm is the permittivity of muscle tissue.

The relative absorption cross section (RAC) is defined as the ratio of the AC to the geometrical cross section G, where G is the body's crosssectional area projected onto a plane perpendicular to the direction of propagation of the incident wave (e.g., G = pia2 for a sphere of radius a). The RAC is a dimensionless number and is a measure of the object's ability to absorb EM energy. For an arbitrarily shaped body, the RAC depends on the orientation of the body with respect to the polarization of the EM fields. In terms of the average SAR, it can be expressed as

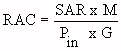equation(Equation 5.26)

The relative scattering cross section (RSC) is defined as

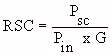equation (Equation 5.27)

where Psc is the total power scattered by the object. The RSC shows how effective the geometric cross section is in scattering the power it intercepts. Graphs of the RAC are shown in Figure 5.8 for prolate spheroidal models of an average man, a rabbit, and a medium-sized rat--in the frequency range from 10-105 MHz and for the most highly absorbing polarization, E polarization. The data in Figure 5.8 show that the RAC is a strong function of frequency and shape; also, near resonance the effective cross-sectional area in terms of total energy absorbed is greater than the geometric cross section of the body. Figure 5.9 shows the RAC and the RSC for a prolate spheroidal model of a medium rat.
At low frequencies the RSC varies as f 4 ; this is called the Rayleigh scattering region. Rayleigh scattering is independent of the shape of the object. Also at low frequencies the size of the object is small compared to a wavelength, the object does not interact strongly with the EM fields, and the RAC and RSC are therefore both very small. Near resonance, where the length of the object is about a half-wavelength, the interaction is very strong and both the RAC and the RSC are greater than unity. For the model of Figure 5.9, near resonance the RSC is greater than the RAC, which means that this model is a more effective scatterer than absorber.

Figure 5.8.
Relative absorption cross section in prolate spheroidal models of an average man, a rabbit, and a medium-sized rat--as a function of frequency for E polarization.

Figure 5.9.
Comparison of relative scattering cross section (RSC) and relative absorption cross section (RAC) in a prolate spheroidal model of a medium rat--for planewave irradiation, E polarization.

The three graphs shown in Fig. 5.8 would lie almost on top of each other if they were normalized to the resonant frequencies, which suggests a possibility of a universal RAC graph. Our calculations showed, however, that the graphs are probably not close enough to make a universal curve useful except possibly for very approximate estimates.

5.1.5. Qualitative Dosimetry

Since calculating dosimetric data is usually difficult, time consuming, and expensive, obtaining the desired dosimetric information for a given experiment or application is not always possible. Often, therefore, just having a rough estimate of the dosimetric results to be expected would be useful, both to decide whether further work is justified and to guide and check experiments. This is especially true for near-field dosimetry.
Researchers doing experiments that involve near-field irradiation are apt to find that the near-field SAR curves in this handbook do not correspond closely to those for their irradiation conditions. Near-field radiation varies greatly from source to source, and we have no ready way to normalize the calculated SARs to the incident fields, as we have for planewave irradiation. Consequently it is not practical to give a set of normalized near-field SAR curves to use for predicting SARs in specific experiments, as it is for planewave SARs. However, by having near-field SARs for some typical simple sources (as given in Chapter 6), along with qualitative explanations of how the near-field SARs are related to the incident fields, we can at least predict relative values of SARs for given exposure conditions. In this section, some of the basic characteristics of EM fields described in Chapter 3 are used to develop in more detail some techniques for estimating relative values of SARs, both for far-field and near-field irradiation. These techniques are based on two qualitative relations described earlier: the boundary conditions on the E-field and the magnetic flux intercepted by the absorber.

Estimating Values of internal Fields--As explained in Chapter 3, at a boundary between two media with different complex permittivities, the E-field must satisfy the following two boundary conditions:

E1p = E2p (Equation 5.28)

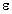epsilon1E1n = 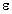epsilon2E2n (Equation 5.29)

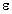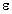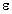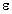where Elp and E2p are components parallel to the boundary, and Eln and E2n are component, perpendicular to the boundary, as shown in Figure 5.10. It is important to remember that Equations 5.28 and 5.29 are valid only at a point on the boundary. From Equation 5.29, we can see that E2n = epsilon1 Eln /epsilon2; and if epsilon2 >> epsilon1, then E2n << E1n. 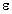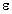Thus if Eln is the field in free space and E2n is the field in an absorber, the internal field at the boundary will be much weaker than the external field at the boundary when epsilon2 > > epsilon1 and the fields are normal to the boundary. Also, from Equation 5.28, we see that the external field and the internal field at the boundary are equal when the fields are parallel to the boundary. These two results will be used extensively in explaining relative energy absorption.

Figure 5.10.
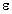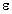Field components at a boundary between two media having different complex permittivities, epsilon1 and epsilon2.

Boundary conditions are not as important on the H-field as on the E-field for explaining relative energy absorption in biological materials because they are usually nonmagnetic (mu = muo ) and have no significant effect on the H-field itself at the boundary. Another relation between the incident H-field and the internal E-field, however, is useful in explaining qualitatively the relative strengths of internal fields.
From the integral form of Maxwell's equation,

equation (Equation 5.30)

For the very special case of a lossy dielectric cylinder in a uniform H-field Equation 5.30 can be solved by deducing from the symmetry of the cylinder and fields that E will have only a phi component that will be constant around a circular path, such as the one shown dotted in Figure 5.11. For E constant along the circular path, and H uniform, Equation 5.30 reduces to

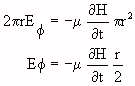equation (Equation 5.31)

Thus, Equation 5.30 shows that E is related to the rate of change of the magnetic flux intercepted by the object; and Equation 5.31 shows that for the very special case of Figure 5.11, the E-field circulates around the H-field and is directly proportional to the radius. For this example the circulating E-field (which produces a circulating current) would be larger for a larger cross section intercepted by the H-field. The generalized qualitative relation that follows from Equation 5.30 is that the circulating field is in some sense proportional to the cross-sectional area that intercepts the H-field. This result is very useful in qualitative explanations of relative energy absorption characteristics; however, this qualitative explanation cannot be used indiscriminantly.

Figure 5.11.
A lossy dielectric cylinder in a uniform magnetic field.

The qualitative relations obtained above from the boundary conditions on E and the circulating E-fields produced by H can be used to explain the relative energy-absorption characteristics in terms of some relations that are strictly valid only at low frequencies. The qualitative explanations thus derived, however, appear to be useful at higher frequencies also.
At lower frequencies the internal fields can be thought of as being generated by the incident E and incident H separately. That is, there will be two sets of internal , E-fields: one generated by the incident E and one generated by the incident H. The total internal E-field is the sum of these two internal E-fields, i.e.,

Ein = E e+ Eh (Equation 5.32)

where

Ee = The internal E-field generated by Einc (incident E-field)
Eh = The internal E-field generated by Hinc (incident H-field)
Ein = The total internal E-field
Ee = The magnitude of the vector field Ee (with similar notation for Eh , Ein , and other vectors)
At low frequencies Ee can be calculated from Einc , and Eh from Hinc and the two are added as in Equation 5.32 to obtain Ein. This procedure cannot be followed, however, at the higher frequencies, where the E- and H-fields are strongly coupled together by Maxwell's equations. Instead, Ee and Eh are strongly interactive and must be calculated simultaneously. However, the qualitative explanations based on the separate calculations of Ee and Eh and the use of Equation 5.32 seem to have some validity at higher frequencies, perhaps even up to resonance in some cases.
The basis for qualitative explanations of the relative strength of Ein can be based on two qualitative principles (QP):

QP1.
Ee is stronger when Einc is mostly parallel to the boundary of the object and weaker when Einc is mostly perpendicular to the boundary of the object.

QP2.
Eh is stronger when Hinc intercepts a larger cross section of the object and weaker when Hinc intercepts a smaller cross section of the object.

Figure 5.12 shows some examples of qualitative evaluations of internal fields based on these principles. For clarity only simple objects are shown in the illustrations, but the principles can be used with more complicated shapes (e.g., the human body). The dependence of the planewave SAR on polarization can be explained on the basis of QPl and QP2, as illustrated by the summary in Table 5.1 (refer to Figure 3.37 for the orientations of the incident fields for each polarization).

Figure 5.12.
Qualitative evaluation of the internal fields based on qualitative principles QPl and QP2. Ee is the internal E-field generated by Einc, the incident E-field, and Eh is the internal E-field generated by Hinc,the incident H-field.

Table 5.1
Application of QP1 and QP2 To Planewave SARS

Since Ee and Eh are both strong for E polarization, its relative SAR is the highest. The weak Ee and Eh make the relative SAR of H polarization the lowest, with that of K polarization between the two. Note that for H polarization the cross section intercepted by Hinc is circular, also smaller than the elliptical cross section intercepted by Hinc in E and K polarization.
From the limited amount of available near-field absorption data, QPI and QP2 appear also to be very useful in explaining near-field dosimetric characteristics. For example, consider Figure 8.20, the measured relative SAR in man and monkey spheroidal models irradiated by a short electric monopole antenna on a ground plane. 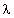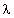At first it may seem surprising that the SAR-fields increases more slowly than (lambda/d)2 , since the magnitude of the E- and H-fields is expected to increase more rapidly than lambda/d in the near-field region. However, the reasons for the shape of the SAR curve may be found from Figure 8.21, which shows the behavior of the measured fields of the antenna (designated Einc and Hinc with respect to an absorber). 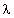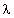The direction of the Hinc does not change with d, but the magnitude of Hinc increases faster than lambda/d for d/lambda < 0.3. The direction of Einc however, changes significantly with d. 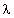In the far field, the angle alpha between Einc and the long axis of the spheroid is zero; but at d/lambda = 0.1, it is about 70º. 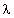According to QP1, this change in angle has a significant effect on Ee Thus the change in SAR with d/lambda results from three factors:

  1. Ee increases as the magnitude of Einc increases.

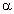  2. Ee decreases as alpha increases.

  3. Eh increases as the magnitude of Hinc increases.
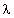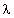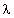Even though Eh increases faster than lambda/d, Ee increases much more slowly than lambda/d because of the combination of factors 1 and 2. The average SAR, which is proportional to E2in does not increase as fast as (lambda/d)2 because Ee affects Ein more than Eh does. On the other hand, since the monkey-size spheroid is relatively shorter and fatter than the man-size spheroid, Eh has a stronger effect on Ein for the monkey than for the man. Consequently, the SAR for the monkey increases more rapidly as d decreases than does the SAR for the man.
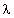Similarly, the variation of the relative SARs in Figure 6.31 can be explained in terms of the antenna-field behavior, as shown in Figures 6.37- 6.39. In Figure 6.31 the relative SAR curves for 10, 27.12, 50, and 100 MHz lie very close together, while those for 200 and 300 MHz differ significantly for some values of d/lambda. The reasons for this can be seen from Figures 6.37 - 6.39:
  1. Einc is slightly lower at 200 MHz and significantly lower at 300 MHz than at the other frequencies.
  2. Hinc is lower at 200 and 300 MHz than at the other frequencies.
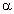  3. The angle alpha of Einc with the z axis is significantly higher at 200 and 300 MHz than at the other frequencies.
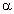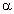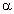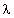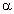Einc is not the strongest factor since it is not much less at 200 than at 100 MHz, but the relative SAR is significantly less at 200 MHz than at 100. The dominant factor is alpha. According to QP1, as alpha increases, the SAR decreases. The effect of alpha can be seen from the 300-MHz curve which begins to rise rapidly at y/lambda = 0.3, where alpha decreases steeply. A surprising aspect of the correspondence between incident-field characteristics and the relative SAR characteristics is that the correlation was based on the values of the incident fields at only one point in space.
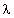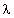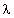Some other important SAR characteristics are the differences between the relative SARs for K and H polarization (Figures 6.32, 6.33) as compared to E polarization (Figure 6.31). 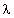Although the variation of the Einc with respect to lambda/y (as shown in Figure 6.37) for 0.15 < y/lambda < 0.5 is slower than lambda/y, the relative SARs for an absorber at distance d from the dipole for both H and K polarizations vary faster than (lambda/d)2 in this region (as seen in Figures 6.32 and 6.33). From the nature of the incident fields (as shown in Figures 6.37-6.39), Eh appears to dominate for K and H polarizations, while Ee dominates for E polarization. The same behavior is shown in a different way in Figure 5.13, where the calculated average SAR for a prolate spheroidal model of an average man is shown as a function of eta = Einc/etao Hinc , the normalized field impedance, with Einc constant at 1 V/m. The curves show the characteristic behavior that results when the impedance deviates from the planewave case (eta = 1). Since Einc is constant, small eta means large Hinc ; thus, for a very small eta , Hinc dominates and E polarization and K polarization become equivalent.
The important information furnished by the curves in Figure 5.13 is that the SAR changes significantly with the Hinc field for K and H polarizations, but changes very little with the Hinc for E polarization in the range 0.5 < eta < 1.5, which, according to Figure 6.40, is the range of interest. This means that the contribution of the Hinc to the average SAR dominates for K and H polarizations, while the contribution of the Einc dominates for E polarization, as explained by Durney et al. (1975) and in the report by the National Council on Radiation Protection and Measurements (1981). 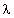Thus, for K and H polarization, the SAR in the long-wavelength region follows the Hinc variation and therefore lies above the (lambda/d)2 variation, as shown in Figures 6.32 and 6.33.
Further insight at low frequencies is provided by the information in Figure 5.14, which shows the ratio of the SAR produced by Ee to that produced by Eh for a 0.07 -m3 prolate spheroidal model at 27.12 MHz for each of the three polarizations. For a/b < 3.5, Eh dominates in all three polarizations; but for a/b > 3.5, Ee dominates in E polarization and Eh dominates in H and K polarization. This is shown only for a conductivity of 0.4 S/m and at low frequencies, but it appears that Eh usually dominates in H and K polarization, while Ee dominates in longer, thinner models for E polarization. Note that QPI and QP2 cannot be used to compare Ee and Eh for different polarizations; they can be used only to compare the Ee for one set of conditions to the Ee for another set, and the Eh for one set of conditions to the Eh for another set.

Figure 5.13.
Average SAR in a prolate spheroidal model of an average man as a function of normalized impedance for each of the three polarizations. (a = 0.875 m, b = 0.138 m, f = 27.12 MHz, 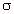sigma = 0.4 S/m, incident E-field is 1 V/m.)

Figure 5.14.
Ratio of (SAR)e, to (SAR)h of a 0.07-m3 prolate spheroid for each polarization as a function of the ratio of the major axis to the minor axis of the spheroid at 27.12 MHz, 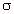sigma = 0.4 S/m.

blue line

Go to Chapter 5.2

Return to Table of Contents.

Last modified: June 14, 1997
© October 1986, USAF School of Aerospace Medicine, Aerospace Medical Division (AFSC), Brooks Air Force Base, TX 78235-5301

This is a Department of Defense computer system for authorized use only. DoD computer systems may be monitored for all lawful purposes, including to ensure that their use is authorized, for management of the system, to facilitate against unauthorized access, and to verify security procedures, survivability, and operational security. Using this system constitutes consent to monitoring. All information, including personal information, placed on or sent over this system may be obtained during monitoring. Unauthorized use could result in criminal prosecution.

POC: AFRL/HEDM, (210)536-6816,  DSN 240-6816