7.2.6. Scaled-Model Techniques

blue line
Although measurements in models made of tissue-equivalent material are valuable for determining the internal distribution of SARs and E-fields, making measurements in full-size models of people and larger animals is often difficult. A useful alternative is to make measurements on smaller models at higher frequencies and then relate these measured values to corresponding values that would occur in the full-size models. This process is called scaling.
Measurements on scaled models offer several advantages over measurements on full-size models:
  1. In the smaller models less electromagnetic generator power is required to produce measurable temperature rises. in full-size models excessive amounts of power are often required to produce measurable temperature rises, especially enough rise to measure heating patterns accurately in the presence of thermal diffusion.
  2. Use of several scaled models permits measurements at more frequencies. Since most lectromagnetic generators with sufficient power are narrow-band, measurements in full-size models can usually be made only over a very narrow frequency band
  3. Scaled models are smaller, easier to handle, and less expensive than full-size models.

Mathematical basis for Measurements on Scaled Models--The derivation of relations between quantities in the full-size and scaled system is outlined here. Readers interested only in the results should skip to the next subsection.

Since scaling is based on the linearity of Maxwell's equations, it is valid only for linear materials. With respect to typical measurements of SAR and E-field distributions, biological materials are linear. Scaling is valid for inhomogeneous materials--materials whose properties vary from point to point--as long as the material is linear at each point.
To derive the relations between measurements in the full-size and scaled models, let each point in full-size model A (Figure 7.4) be described by coordinates x, y, and z and each point in scaled model à be described by coordinates tilde x, tilde y and tilde z.

Figure 7.4.
Schematic diagram illustrating the coordinate system used in the scaling procedure. (a) Fullsize object with coordinate system x, y, z; (b) scaled model with coordinate system 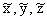tilde x, tilde y and tilde z.

Each point in à is obtained by reducing the coor-dinates of a point in A by the scale factor S. Therefore, the coordinate values are related by

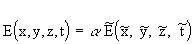equation (Equation 7.10)
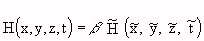equation (Equation 7.11)
equation (Equation 7.12)

Since four fundamental quantities--mass, length, time, and charge--are required to describe an electromagnetic-field quantity, three scale factors in addition to S are required to relate quantities in à to those in A. Scale factors for E- and H-fields, however, are more convenient than those for mass and charge. Hence the following additional three scale factors have traditionally been used:

equation(Equation 7.13)
equation(Equation 7.14)
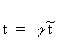equation(Equation 7.15)


where E is electric field; H is magnetic field; t is time; and 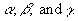symbols are the corresponding scale factors.
Desired relationships between quantities in full-size and scaled system can be found from Maxwell's equations because the fields in both systems must satisfy them. For simplicity, development of the relationships will be described for sinusoidal steady-state electromagnetic fields. This is appropriate because most measurements in biological systems are of sinueoidal steady-state quantities. For this case, the fields in the full-size system must satisfy

equation(Equation 7.16)
equation(Equation 7.17)

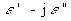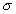where symbol is the complex permeability and symbol is the complex relative permittivity (see Sections 3.2.6, 3.3.3, and 4.1). The effective conductivity, symbol, is related to e" by

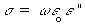equation (Equation 7.18)

Fields in the scaled model, on the other hand, must satisfy

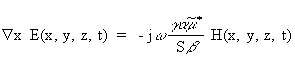equationEquation (7.19)
equation(Equation 7.20)


where symbol indicates differentiations with respect to tilde x, tilde y, and tilde z
If the scaled model is an accurate simulation of the full-size system, then substituting the transformations relating scaled-model quantities to the full-size model should transform Equations 7.19 and 7.20 into 7.16 and 7.17 respectively. Substituting Equations 7.10-7.15 into 7.19 and 7.20 gives
equation (Equation 7.21)
equation (Equation 7.22)

Note that

equation (Equation 7.23)
equation (Equation 7.24)

Equations 7.21 and 7.22 will be the same as 7.16 and 7.17, respectively, if

equation(Equation 7.25)
equationEquation 7.26)

If material properties and scaling factors are selected so that Equations 7.25 and 7.26 are true, then measured quantities in the scaled model can be related to those in the full-size system, because Equations 7.19 and 7.20, which describe fields in the scaled system, are equivalent to Equations 7.16 and 7.17, respectively, which describe fields in the full-size system.

Scaling factors can be chosen as follows. First, since biological materials are essentially nonmagnetic, the symbol and symbol are both approximately equal to symbol . Therefore, from Equation 7.25,

equation(Equation 7.27)

Second, it is most convenient to have both the full-size and the scaled models surrounded dby air. Then Equation 7.26 must be valid when both equation and equation represent air; that is equation From Equation 7.26 for this condition,

equation(Equation 7.28)

Equations 7.27 and 7.28 together require

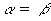equation (Equation 7.29)
equation(Equation 7.30)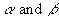

The specified conditions thus far have been based on making field patterns correspondingly similar in full-size and scaled models by requiring solutions to Maxwell's equations in the two cases to correspond. Complete specification of electromagnetic fields requires the fields to satisfy Maxwell's equations and boundary conditions. The next step, then, is to specify symbols from boundary conditions. This is equivalent to adjusting the intensity of the electromagnetic sources in the two systems. The usual practice is to set

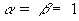equation(Equation 7.31)

which is equivalent to making the intensity of the source fields in the two systems equal. This can be seen from Equations 7.13 and 7.14, which are valid for all pairs of coordinate points (x, y, z, t) and 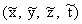symbols. Let the corresponding points be far enough away from the object so that scattered fields are negligibly small and only source fields are present. Then, symbolscorresponds to the source fields in the two systems having equal intensities. This assumes that the sources in the two systems are correspondingly similar. 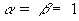Since scattered-field intensities are proportional to source field intensities, the interpretation that "setting equationis equal to making the source intensities equal" is valid at all points but easier to understand at points where the scattered fields are negligible.

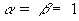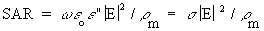With the scaling parameters specified by Equations 7.30 and 7.31, measured quantities in the scaled model can be related to measurements in the full-size model. Local SAR is of particular interest. From Equation 3.49, the SAR at a point in the full-size model is where symbolis mass density.

equation(Equation 7.32)

The relationship with the effective conductivity, symbol, is usually used. From Equations 7.26, 7.30, and 7.31,

equation (Equation 7.33)

Relating symbol and symbol to symbol and symbol (see Equation 7.18),

equation

Using Equation 7.23 gives

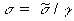equation(Equation 7.34)

and using Equation 7.30 gives

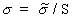equation (Equation 7.35)

From Equations 7.32, 7.13, and 7.34, the general relationship for SAR is

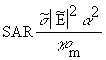equation(Equation 7.36)
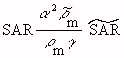equation(Equation 7.37)

When both models are in air and the intensities of the sources are equal (so Equations 7.30 and 7.31 apply) and for the usual case when 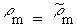equation, Equation

7.37 reduces to

equation(Equation 7.38)

From Equation 7.38, the scaled-model SAR is seen to be higher than that in the full-size model by scale factor S. This is often a significant advantage because it generally means that making measurements in a scaled model requires less generator power. This is particularly important when temperature measurements are made because it means that less power is required to get a measurable temperature rise in a scaled model than in a full-size model.

Another quantity that sometimes is of interest is the Poynting vector. The scaling relationship is easily obtained from Equations 7.13 and 7.14:

equation(Equation 7.39)
Applications of ScalingRelationships--The general scaling relationships derived above are summarized in Table 7.14 in terms of the various factors. The relationships for commonly used values of the scale factors are given in Table 7.15. In practice, the scaling factor is usually determined by the desired irradiation frequency of the full-size model and the frequency at which the scaled model could be irradiated. For example, the SAR distribution at 13.56 MHz in a 0.52-m-diameter spherical model of equivalent muscle tissue might be desired, and a generator with sufficient power for measurements at 100 MHz is available. The appropriate scale factor, S, and the other parameters are given in the example in Table 7.15.

Adjusting the conductivity of the model material is often important in scaling techniques, as illustrated in Table 7.15. This can usually be done by varying the amount of NaCl in the mixture. Fortunately the amount of NaCl can be varied enough to adjust 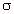sigma without affecting symbol drastically. Figure 7 .5 shows conductivity as a function of percentage of NaCl for various percentages of the gelling agent TX-150 (see Section 7.2.5). Doubling the percentage of TX-150 has a relatively small effect on the conductivity, which is largely controlled by the percentage of NaCl. Figures 7.6 and 7.7 show the conductivity values as a function of percentage of NaCl. These graphs can be used to simulate muscle tissue in saline form for a wide range of frequencies and scale factors.

Table 7.14.
General Scaling Relationships

Table 7.15.
Scaling Relationships For Typical Values Of Scaling Parameters

Figures 7.5 and 7.6
Electrical conductivity of phantom muscle as a function of NaCl and TX-150 contents measured at 100 kHz and 23°C.

Figure 7.6
Electrical conductivity of saline solution as a function of the aqueous sodium chloride concentration.

Figure 7.7
Electrical conductivity of saline solution as a function of the NaCl concentration at 25ºC.

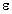Table 7.16 shows nine compositions that can be used to simulate muscle material over a wide range of parameters. For example, to get a conductivity of symbol = 4.6 S/m, Figure 7.5 shows that the NaCl concentration should be about 3.5% of the total mixture. From Table 7.16, we see that mixture VIII could be adjusted to accommodate the 0.4% difference needed in NaCl concentration. The epsilon' for the mixtures in Table 7.16 are all about that of water. 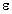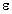In many cases the epsilon" for biological tissue is the dominant factor in determining the SAR, especially at frequencies from 10 to 20 MHz, and the value of epsilon' is not critical to the measurements.

Table 7.16.
Compositions of the Nine Mixtures Used for Measuring Dielectric Properties

7.3. TABULATED SUMMARY OF PUBLISHED WORK IN EXPERIMENTAL DOSIMETRY

Table 7.17 contains a summary of published work in experimental dosimetry, including references.

Table 7.17
A Summary of Available Experimental Data on Fields and SAR Measurements in Biological Phantoms and Test Animals Irradiated by Electromagnetic Fields


blue line

Go to Chapter 8.

Return to Table of Contents.

Last modified: June 14, 1997
© October 1986, USAF School of Aerospace Medicine, Aerospace Medical Division (AFSC), Brooks Air Force Base, TX 78235-5301

This is a Department of Defense computer system for authorized use only. DoD computer systems may be monitored for all lawful purposes, including to ensure that their use is authorized, for management of the system, to facilitate against unauthorized access, and to verify security procedures, survivability, and operational security. Using this system constitutes consent to monitoring. All information, including personal information, placed on or sent over this system may be obtained during monitoring. Unauthorized use could result in criminal prosecution.

POC: AFRL/HEDM, (210)536-6816,  DSN 240-6816