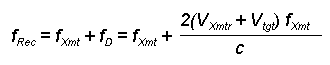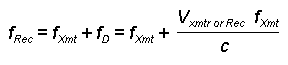Doppler frequency shift is
directly proportional to velocity and a radar system can therefore be calibrated to measure
velocity instead of (or along with) range. This is done by measuring the shift in frequency of a
wave caused by an object in (figure 2).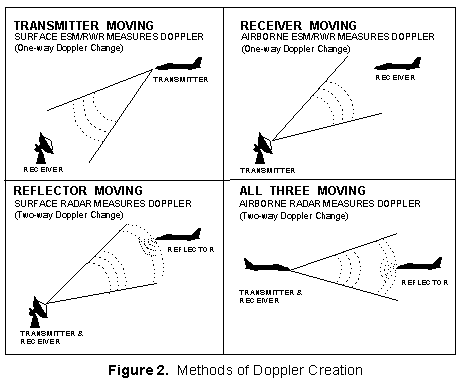
* Transmitter in motion
* Reflector in motion
* Receiver in motion
* All three
For a closing relative velocity:
* Wave is compressed
* Frequency is increased
For an opening relative velocity:
* Wave is stretched
* Frequency is decreased
To compute Doppler frequency we note that velocity is range rate; V = dr/dt
For the reflector in motion case, You can see the wave compression effect in figure 3
when the transmitted wave peaks are one wavelength apart. When the first peak reaches the
target, they are still one wavelength apart.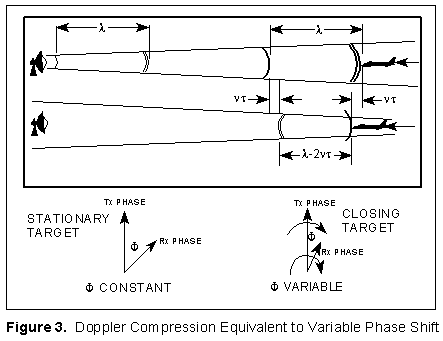
When the 2nd peak reaches the target, the target has advanced according to its velocity (vt), and the first reflected peak has traveled toward the radar by an amount that is less than the original wavelength by the same amount (vt).
As the 2nd peak is reflected, the wavelength of the reflected wave is 2(vt) less than the original wavelength.
The distance the wave travels is twice the target range. The reflected phase lags transmitted phase by 2x the round trip time.
For a fixed target the received phase will differ from the transmitted phase by a constant phase shift. For a moving target the received phase will differ by a changing phase shift.
For the closing target shown in Figure 3, the received phase is advancing with respect to the transmitted phase and appears as a higher frequency.
Doppler is dependent upon closing velocity, not actual radar or target velocity as shown in Figure 4.
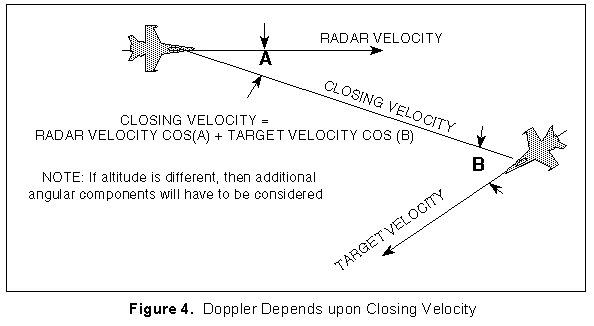
For the following examples, we assume the radar and target are moving directly toward one another in order to simplify calculations (Use the velocity component of one in the direction of the other for the formulas).
For the case of a moving reflector, doppler frequency
is
proportional to 2x the transmitted frequency:
Higher rf = higher doppler shift
fD = (2 x VTarget)(f/c)
Likewise, it can be shown that for other cases, the following relationships hold:
For an airplane radar with an airplane target , (The
"all three moving" case)
fD = 2 x( VRadar +
VTarget)(f/c)
For the case of a semi-active missile receiving signals
(also "all three moving")
fD = ( VRadar + 2VTarget + VMissile)(f/c)
For the airplane radar with a ground target (radar
mapping)
fD = 2( VRadar Cos P Cos
Q)(f/c), Where P and Q are the radar scan azimuth and depression angles.
For the ES/ESM/RWR case where only the target or receiver is
moving (One-way
doppler measurements)
fD = VReceiver or Target
(f/c)
Figure 5 depicts the results of a plot of the above equation for a moving reflector such as might be
measured with a ground radar station illuminating a moving aircraft.
It can be used for the aircraft-to-aircraft case, if the total net closing rate of the two aircraft is used for the speed entry in the figure.
It can also be used for the ES/ESM case (one-way doppler measurements) if the speed of the aircraft is used and the results are divided by two.