Die Mandelbrot Menge

Das Mandelbrot Fraktal ist wohl das bedeutendste und bekannteste Fraktal im
Zusammenhang mit dem Begriff "Chaos-Theorie". Es ist nicht nur
schön, sondern gibt der Mathematik auch neue Rätsel auf.
Das Mandelbrot Fraktal wurde von Dr. Benoit Mandelbrot (IBM) "gefunden".
Überlegungen zu chaotischen Systemen lassen sich ziemlich genau auf den
französischen Mathematiker Gaston Julia zurückführen. Er untersuchte
als erster die Funktion xn+1 = x2 + c. Dabei fand er heraus,
das wiederholte Einsetzung unvorhersagbare, "chaotische" Werte
lieferte. Julia selbst konnte damals (1919) noch nicht erkennen, welche Tragweite
seine Entdeckung haben sollte. Erst durch den Einsatz von leistungsstarken
Computern konnte Anfang der siebziger Jahre Benoit Mandelbrot der Entdeckung
zu nachträglichem Ruhm verhelfen.
Das Mandelbrot Fraktal ist das Geometrische Abbild der Mandelbrot Menge. Die
Mandelbrot Menge ist eine Zahlenmenge in der Zahlenmenge der Komplexen Zahlen.
Für jede komplexe Zahl C wird definiert:
Z0 = 0 + 0i
Zn+1 = Zn2 + C
Die komplexe Zahl C ist dann und nur dann Teil der Mandelbrotmenge, wenn
|Zn| endlich für alle n e N ist.
Um die Mandelbrotmenge geometrisch auf einem Computer darzustellen, teilt man
jedem Bildpunkt auf dem Computermonitor ("Pixel" = PIcture ELement)
eine komplexe Zahl zu. Für jede so entstandene komplexe Zahl wird dann
überprüft, ob Zn für die ersten 1000 Iterationen
(Wert kann geändert werden, grössere Werte ergeben genauere
Ergebnisse, benötigen aber auch mehr Rechenzeit) einen Betrag kleiner als 2
hat.
Es kann gezeigt werden, dass, wenn irgendein Zn einen Betrag größer
als 2 hat, Zn für n gegen unendlich auch |Zn| gegen
unendlich geht.
Wenn C nun diese Bedingung erfüllt, so kann mit hoher Wahrscheinlichkeit
angenommen werden, das C Teil der Mandelbrotmenge ist, und der Pixel wird
schwarz gefärbt (Auf dem Bild oben weiss). Wenn C jedoch nicht Teil der Menge ist (also wenn
|Zn| > 2 ist), dann wird ihm eine andere Farbe zugeteilt. Im
einfachsten Falle ist es weiß. Bunte Abbilder der Mandelbrotmenge
erhält man, wenn man dem Pixel je nachdem, bei welchem n |Zn| zum
ersten Mal größer als 2 war eine andere Farbe zuteilt (kleine n Werte = weite Entfernung vom
Mandelbrot Fraktal, große n Werte = nahe am Fraktal dran).
Fakten zur Mandelbrotmenge:
- Die gesamte Mandelbrotmenge ist verbunden
- Die Fläche der Mandelbrotmenge: 1.5065923 +- 0.0000006 LE2
- Alle Sub-Mandelbrotmengen sind ähnlich, aber immer leicht von der Ursprungsform abweichend
- Die Mandelbrotmenge ist komplett in einem Kreis mit dem Radius 2 um 0 + 0i.
Die Julia Menge
Die Julia Menge (nach oben genannten frz. Mathematiker Gaston Julia benannt) wird
auf die gleiche Weise wie die Mandelbrotmenge gebildet, nur das nicht die Zahl,
auf der die Iteration basiert, selbst addiert wird, sondern eine für
das gesamte Bild geltende Konstante. Durch Ändern dieser Konstante
erhält man viele verschiedene Julia Mengen. Legt man die Mandelbrot und
Julia Mengen übereinander, so erkennt man den Zusammenhang zwischen beiden:
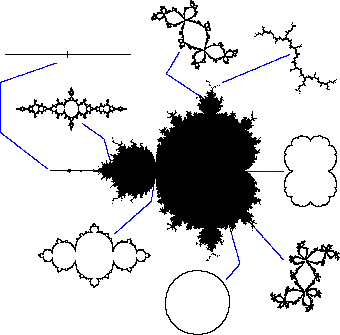
Die äusseren Mengen sind jeweils Julia Mengen. Die Striche zeigen an,
wo die Konstante (als komplexe Zahl) in der Mandelbrotmenge zu finden ist.
Unten in der Mitte ist die Additionskonstante 0 + 0i, die Julia Menge mit
dieser Konstante ist kreisförmig.
Man findet bei entsprechender Vergrößerung sowohl Julia Untermengen in
der Mandelbrot Menge als auch umgekehrt.

