Zufall, Vorhersagbarkeit, Entropy

Warum braucht man "zufällige" Zahlen ?
Zufällige Zahlen werden für eine Reihe von alltäglichen Anwendungen im Computerbereich benötigt, zum Beispiel bei statistischen Analysen, bei Spielen, um möglichst unvorhersehbar zu handeln, und bei der Datenverschlüsselung (Kryptographie).

Wann ist eine Zahl "zufällig" ?
Im ersten Augenblick mag diese Frage sehr leicht zu beantworten klingen, aber hier sind ein paar Beispiele, warum es schwer ist eine allgemein gültige Definition zu finden:

1.	1111111...	Nicht zufällig, da es nur eine mögliche Ziffer gibt.
2.	123123123...	Nicht zufällig, da periodisch vorhersagbar ist.
3.	141592653	Nicht zufällig, da Bildungsregel ersichtlich.
4.	937393793...	Nicht zufällig, da nur die Ziffern 9, 3 und 7 vorkommen.
5.	1234567890...	ist nicht zufällig, da zwar alle Ziffern (statistisch) gleich häufig vorkommen, aber die Wahrscheinlichkeit, das die 8 hinter der 7, die 7 hinter der 6, usw. kommt 100% ist.

"Für jede Ziffer ist das Auftreten an jedem Ort gleich wahrscheinlich und es ist unmöglich selbst bei Kenntnis aller Umstände und vorher aufgetretenen Zufallszahlen die nächste Ziffer vorherzusagen." ist eine relativ gute Definition [1,4].

Daraus folgt, das eine wirkliche Zufallszahl, die theoretisch unendlich lang ist, in kein statistisches Muster paßt, so sollte es auch unmöglich sein sie zu komprimieren, d.h. sie durch irgendwelche Bildungsregeln oder statistische Methoden zu verkleinern, ihre Entropy liegt bei Null. Entropy ist das Maß für die Menge an Regeln die in den Daten herrscht. Findet man die richtigen Bildungsregeln für die Daten, lassen sie sich verkleinern, um so kleiner die Entropy ist, desto schwieriger wird es, Daten zu komprimieren [4].

Solange die Datenmenge endlich ist, kann keine genaue Aussage über die Entropy gemacht werden, wenn sie jedoch unendlich groß ist, so dauert auch eine Überprüfung unendlich lange.

Zufall durch den Computer
Da ein Computer strikten Regeln folgt, ist es sehr schwer auf ihm "brauchbare", also relativ unvorhersagbare Zufallszahlen zu generieren. Sobald man eine Formel oder einen Algorithmus verwendet besteht die Möglichkeit der Vorhersagbarkeit [2].
Es gibt zwar "echte" Zufallsgeneratoren, wie zum Beispiel die Auswertung von atmosphärischem Rauschen, oder die Umwandlung von Radiowellen, jedoch sind diese Methoden sehr aufwendig und teuer, und für den normalen Computernutzer unzumutbar, deshalb wird auf sogenannte "Pseudo Random Number Generators", kurz PRNG's zurückgegriffen, die rein in Software arbeiten.
PRNG's arbeiten im Allgemeinen nach dem selben Prinzip, sie generieren aus einem wirklich zufälligen Startwert (Millionstel Sekunde seit Computerstart, Mausbewegungen des Users, ...) eine Kette aus anderen Zufallszahlen. Irgendwann wiederholt sich diese Kette, die Länge dieser, sich wiederholenden Kette nennt man Periode des PRNG's. Zwei relativ häufig eingesetzte PRNG's sind nun erklärt:

Lineare Kongruenzgeneratoren (LCG)
Lineare Kongruenzgeneratoren sind mathematisch gesehen Folgen, die aus einem Startwert x0 eine periodische Kette x1,x2, x3,x4,..., xn erzeugen, wobei n die Periode ist.
Die Formel für einen linearen Kongruenzgenerator (LCG) lautet [3]:

xn = (a xn-1 + b) mod m

wobei a der "Multiplikator", b das "Inkrement" und m der Modul ist. Dieser Generator besitzt eine Periode, die höchstens so groß ist wie m. Wurden a, b und m gut gewählt, hat der Generator die maximale Periode m. b sollte relativ prim zu m sein (d.h. keine gemeinsamen Primfaktoren besitzen) [4].
Ein Beispielgenerator:

a = 106, b = 1283, m = 6075. x0 = 4819 (Startwert, willkürlich gewählt), x1 = 1797, x2 = 3440, x3 = 1423, ...

Die statistischen Eigenschaften des Generators, also die Verteilung der Zahlen ist sehr gut, und dieser Generator wird auch oft für statistische Berechnungen eingesetzt. Es stellte sich jedoch heraus, das alle LCG's vorhergesagt werden können [4], daher können sie in der Kryptographie nicht genutzt werden, dennoch sind sie sehr beliebt, da sie sehr leicht in Programmen implementiert werden können.

Wie können solche Generatoren für die Chiffrierung bzw. Kryptographie eingesetzt werden ?
Da die Folge die generiert wird, einzig und allein von dem Startwert x0, und den Konstanten a, b und m abhängt, kann man x0 quasi als "Geheimschlüssel" betrachten. Wenn eine andere Person und ich diesen Schlüssel kennen, kennen wir auch die Folge die daraus entsteht. Diese Folge kann dann mit dem zu verschlüsselnden Text verknüpft werden und so der Chiffretext erzeugt werden. Weitere Informationen unter [4].
Es gibt viele Abwandlungen von Kongruenzgeneratoren [5], die jedoch auf dem selben Prinzip beruhen und hier nicht weiter interessant sind.

Linear Feedback Shifting Register (LFSR)
Eine Zahl, egal ob "REAL" oder "CARDINAL" (Modula 2 Konvention) wird auf dem Computer immer durch einzelne Bits repräsentiert. So hat zum Beispiel eine CARDINAL Zahl auf diesem Linux System 32 Bit, d.h. es können Zahlen bis 2^32 dargestellt werden. Werden alle Bits in einer Zahl (hier einem "Register") um eine Position nach links oder rechts geschoben, was einer Multiplikation bzw. Division mit 2 entspricht, spricht man von "Shifting". Was im ersten Moment kompliziert wirkt, ist eigentlich ganz einfach:
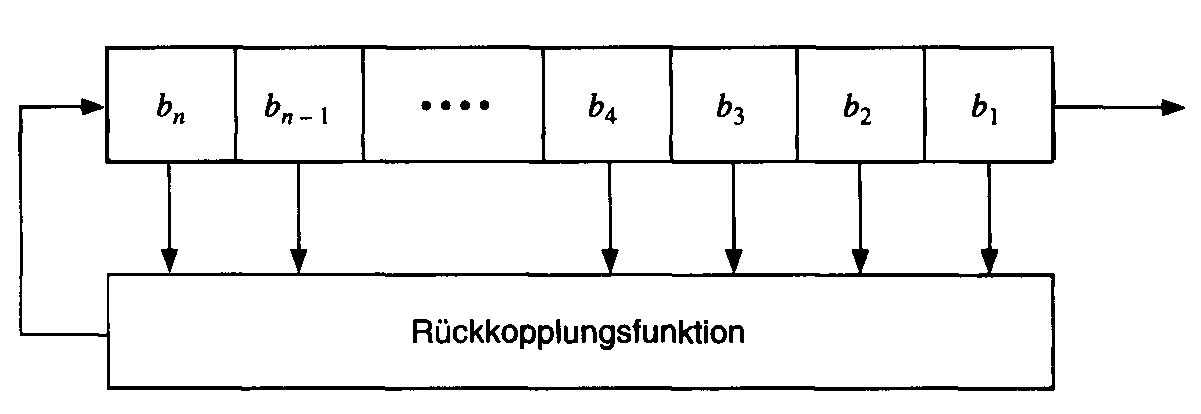Schieberegister mit Rückkopplung [4]
Das Register, also die Zahl, die aus den Bits b1, b2, ..., bn besteht wird immer um eine Position nach rechts geschoben, so das ein Bit einfach "herausfällt". Dann werden alle Bits des Registers mit einer Funktion (z.B. "addiere alle Bits") zu einem Bit verknüpft und in dem freigewordenen Kästchen (Bit) links gespeichert. Als Beispiel soll hier eine ganz einfache Rückkopplungsfunktion verwendet werden, die XOR Function.
Die XOR (exclusive-or, exklusiv-oder) Funktion schnappt sich zwei Bits und vergleicht sie, wenn die Bits verschieden sind, dann gibt die Funktion eine 1 zurück, wenn sie gleich sind eine Null.

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

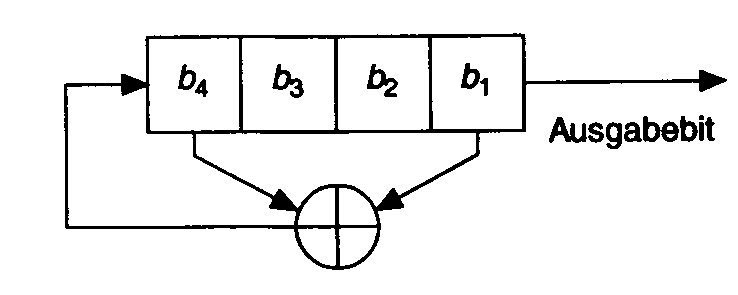4-Bit-LFSR [4]
In der Abbildung ist ein ganz konkretes, 4 Bit LFSR abgebildet. Die Rückkopplungsfunktion besteht darin, das die Bits b4 und b1 XOR-verknüpft werden, und das entstehende Bit von links in b4 geschoben wird, dabei "fällt" b1, unser Zufallsbit rechts heraus.
Als Startwert nehmen wir 1111, d.h. b4, b3, b2 und b1 werden auf 1 gesetzt. Nun werden b4 und b1 verknüpft (1 XOR 1 = 0), und die 0 wird links reingeschoben. Auf der rechten Seite fällt eine 1 heraus. Es entsteht diese Folge:
1111
0111
1011
0101
1010
1101
0110
0011
1001
0100
0010
0001
1000
1100
1110
1111
...
Nur die "rausgefallenen" Bits ergeben diese Zufallskette: 111101011001000...
Die maximale Periode beträgt (2^n) - 1 Bits, im Beispiel (2^4) - 1 = 15 Bits. Man nennt die Angabe der Positionen der Bits, die verknüpft werden (in dem Beispiel 4 und 1) "tap sequence". Werden bestimmte Eigenschaften [4] von der tap sequence erfüllt erhält man sehr gute Generatoren.

Intelligent gewählte LFSR's erzeugen exzellente Zufallsfolgen, die die meisten Zufallstests bestehen. Dennoch sind LFSR's einzeln verwendet mit viel Aufwand vorhersagbar, jedoch in Kombination sind sie kryptographisch sicher, und werden besonders in militärischen Verschlüsselungsalgorithmen eingesetzt, da sie sehr leicht und schnell auch in Hardware umzusetzen sind. Programmiert man einen LFSR, so gibt es eine kleine Abwandlung, "Galois-LFSR" auch g-LFSR, die die Programmierung deutlich vereinfacht und schneller ist (hier nicht aufgeführt).

---

Referenzen

[1]	RFC 1750 - Randomness Recommendations for Security http://www.cis.ohio-state.edu/htbin/rfc/rfc1750.html
[2]	How to Generate Pure Random Numbers http://www.javanet.com/~othello/random.htm
[3]	Linear Congruence Generators http://pw2.netcom.com/~gfull/lincong.htm
[4]	Angewandte Kryptographie, 2. Auflage ISBN 3-89319-854-7
[5]	Congruential Generators http://csep1.phy.ornl.gov:80/rn/node9.html