K using the formula:Repeat..until loop:
Initialization code
Loop body
Test for termination
Code following the loop
While loop:
Initialization code
Loop termination test
Loop body
Jump back to test
Code following the loop
Loop..endloop loop:
Initialization code
Loop body, part one
Loop termination test
Loop body, part two
Jump back to loop body part 1
Code following the loop
As you can see, the repeat..until loop is the simplest of the bunch. This
is reflected in the assembly language code required to implement these loops.
Consider the following repeat..until and while loops that are identical:
SI := DI - 20; SI := DI - 20;
while (SI <= DI) do repeat
begin
stmts stmts
SI := SI + 1; SI := SI + 1;
end; until SI > DI;
The assembly language code for these two loops is:
mov si, di mov si, di
sub si, 20 sub si, 20
WL1: cmp si, di U: stmts
jnle QWL inc si
stmts cmp si, di
inc si jng RU
jmp WL1
QWL:
As you can see, testing for the termination condition at the end of the
loop allowed us to remove a jmp instruction from the loop. This can be significant
if this loop is nested inside other loops. In the preceding example there
wasn't a problem with executing the body at least once. Given the definition
of the loop, you can easily see that the loop will be executed exactly 20
times. Assuming cx is available, this loop easily reduces to:
lea si, -20[di]
mov cx, 20
WL1: stmts
inc si
loop WL1
Unfortunately, it's not always quite this easy. Consider the following Pascal
code:
WHILE (SI <= DI) DO BEGIN
stmts
SI := SI + 1;
END;
In this particular example, we haven't the slightest idea what si contains
upon entry into the loop. Therefore, we cannot assume that the loop body
will execute at least once. Therefore, we must do the test before executing
the body of the loop. The test can be placed at the end of the loop with
the inclusion of a single jmp instruction:
jmp short Test
RU: stmts
inc si
Test: cmp si, di
jle RU
Although the code is as long as the original while loop, the
jmp instruction executes only once rather than on each repetition
of the loop. Note that this slight gain in efficiency is obtained via a
slight loss in readability. The second code sequence above is closer to
spaghetti code that the original implementation. Such is often the price
of a small performance gain. Therefore, you should carefully analyze your
code to ensure that the performance boost is worth the loss of clarity.
More often than not, assembly language programmers sacrifice clarity for
dubious gains in performance, producing impossible to understand programs.
for I := 1 to 8 do for I := 8 downto 1 do
K := K + I - J; K := K + I - j;
mov I, 1 mov I, 8
FLP: mov ax, K FLP: mov ax, K
add ax, I add ax, I
sub ax, J sub ax, J
mov K, ax mov K, ax
inc I dec I
cmp I, 8 jnz FLP
jle FLP
Note that by running the loop from eight down to one (the code on the right)
we saved a comparison on each repetition of the loop. loop instruction (which will improve
the performance of the loop on pre-486 CPUs). jns instruction in place of the jnz instruction
above to repeat the loop some specific number of times:
mov I, 7
FLP: mov ax, K
add ax, I
sub ax, J
mov K, ax
dec I
jns FLP
This loop will repeat eight times with I taking on the values seven down
to zero on each execution of the loop. When it decrements zero to minus
one, it sets the sign flag and the loop terminates.
FOR I := 0 TO N DO
K := K+(I+J-2);
Since J never changes throughout the execution of this loop, the sub-expression
"J-2" can be computed outside the loop and its value used in the
expression inside the loop:
temp := J-2;
FOR I := 0 TO N DO
K := K+(I+temp);
K using the formula:This computation for K is based on the formula:
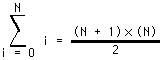
However, simple computations such as this one aren't always possible.
Still, this demonstrates that a better algorithm is almost always better
than the trickiest code you can come up with.
In assembly language, invariant computations are even trickier. Consider
this conversion of the Pascal code above:
mov ax, J
add ax, 2
mov temp, ax
mov ax, n
mov I, ax
FLP: mov ax, K
add ax, I
sub ax, temp
mov K, ax
dec I
cmp I, -1
jg FLP
Of course, the first refinement we can make is to move the loop control
variable (I) into a register. This produces the following code:
mov ax, J
inc ax
inc ax
mov temp, ax
mov cx, n
FLP: mov ax, K
add ax, cx
sub ax, temp
mov K, ax
dec cx
cmp cx, -1
jg FLP
This operation speeds up the loop by removing a memory access from each
repetition of the loop. To take this one step further, why not use a register
to hold the "temp" value rather than a memory location:
mov bx, J
inc bx
inc bx
mov cx, n
FLP: mov ax, K
add ax, cx
sub ax, bx
mov K, ax
dec cx
cmp cx, -1
jg FLP
Furthermore, accessing the variable K can be removed from the loop as well:
mov bx, J
inc bx
inc bx
mov cx, n
mov ax, K
FLP: add ax, cx
sub ax, bx
dec cx
cmp cx, -1
jg FLP
mov K, ax
One final improvement which is begging to be made is to substitute the loop
instruction for the dec cx / cmp cx,-1 / JG FLP instructions. Unfortunately,
this loop must be repeated whenever the loop control variable hits zero,
the loop instruction cannot do this. However, we can unravel the last execution
of the loop (see the next section) and do that computation outside the loop
as follows:
mov bx, J
inc bx
inc bx
mov cx, n
mov ax, K
FLP: add ax, cx
sub ax, bx
loop FLP
sub ax, bx
mov K, ax
As you can see, these refinements have considerably reduced the number of
instructions executed inside the loop and those instructions that do appear
inside the loop are very fast since they all reference registers rather
than memory locations.
FOR I := 3 DOWNTO 0 DO A [I] := 0;
mov I, 3
FLP: mov bx, I
shl bx, 1
mov A [bx], 0
dec I
jns FLP
Each execution of the loop requires five instructions. Only one instruction
is performing the desired operation (moving a zero into an element of A).
The remaining four instructions convert the loop control variable into an
index into A and control the repetition of the loop. Therefore,
it takes 20 instructions to do the operation logically required by four.
A[0]
through A[3]. A more efficient approach is to use four mov
instructions to accomplish the same task. For example, if A
is an array of words, then the following code initializes A
much faster than the code above:
mov A, 0
mov A+2, 0
mov A+4, 0
mov A+6, 0
You may improve the execution speed and the size of this code by using the
ax register to hold zero:
xor ax, ax
mov A, ax
mov A+2, ax
mov A+4, ax
mov A+6, ax
Although this is a trivial example, it shows the benefit of loop unraveling.
If this simple loop appeared buried inside a set of nested loops, the 5:1
instruction reduction could possibly double the performance of that section
of your program.
FOR I := 0 TO 255 DO A [I] := 0;
mov I, 0
FLP: mov bx, I
shl bx, 1
mov A [bx], 0
inc I
cmp I, 255
jbe FLP
Although unraveling this code will still produce a tremendous performance
improvement, it will take 257 instructions to accomplish this task[6],
too many for all but the most time-critical applications. However, you can
reduce the execution time of the body of the loop tremendously using induction
variables. An induction variable is one whose value depends entirely on
the value of some other variable. In the example above, the index into the
array A tracks the loop control variable (it's always equal to the value
of the loop control variable times two). Since I doesn't appear anywhere
else in the loop, there is no sense in performing all the computations on
I. Why not operate directly on the array index value? The following code
demonstrates this technique:
mov bx, 0
FLP: mov A [bx], 0
inc bx
inc bx
cmp bx, 510
jbe FLP
Here, several instructions accessing memory were replaced with instructions
that only access registers. Another improvement to make is to shorten the
MOVA[bx],0 instruction using the following code:
lea bx, A
xor ax, ax
FLP: mov [bx], ax
inc bx
inc bx
cmp bx, offset A+510
jbe FLP
This code transformation improves the performance of the loop even more.
However, we can improve the performance even more by using the loop instruction
and the cx register to eliminate the cmp instruction:
lea bx, A
xor ax, ax
mov cx, 256
FLP: mov [bx], ax
inc bx
inc bx
loop FLP
This final transformation produces the fastest executing version of this
code[7].