- This chapter was revised by Eleanor R. Adair, Ph.D., Associate Fellow, John B. Pierce
Foundation Laboratory, Yale University. It includes material written by James L. Lords,
Ph.D., and David K. Ryser, Ph.D., from previous editions of this handbook and new material
added by Dr. Adair.
10.1. INTRODUCTION
- The study of thermoregulation--the responses that maintain a constant internal body
temperature--has flourished since Claude Bernard (1865) first demonstrated that the
temperature of the blood varies in different parts of the body. Bernard established that
food taken into the body is metabolized in the tissues and that the bloodstream
distributes the released energy throughout the body. The relative constancy of the
internal body temperature was part of his concept of the constancy of the milieu
intérieur, a necessity for optimal functioning and health of the organism. He pointed out
that the vasomotor nerves control the transfer of heat from deep in the body to the skin
and that this is a mechanism of the utmost importance to thermoregulation in homeotherms.
Bernard's discoveries underlie the modern science of thermophysiology and help us to
understand how man and animals can remain relatively independent of the thermal
environment, even when that environment contains potent or unusual thermal stressors.
- Thermal loads on the body can result from changes in metabolic heat production and from
changes in the characteristics of the environment (temperature, ambient vapor pressure,
air movement, insulation, and other environmental variables that may alter the skin's
temperature), Thermalizing energy deposited in body tissues by exposure to radiofrequency
electromagnetic radiation can be a unique exception to the normal energy flows in the
body, although metabolic activity in skeletal muscle can deposit large amounts of thermal
energy directly into deep tissues.
- All living organisms respond vigorously to changes in body temperature. Cold-blooded
animals, called ectotherms because they derive thermal energy mainly from outside the
body, regulate their body temperatures largely through behavioral selection of a preferred
microclimate. Warm-blooded animals, called endotherms because they can produce heat in
their bodies and dissipate it to the environment through physiological processes, often
rely largely on behavioral thermoregulation. Behavior is important to thermoregulation
because it is mobilized rapidly and aids the conservation of body energy and fluid stores.
When behavioral responses--which include the thermostatic control of the immediate
microenvironment--are difficult or impossible, the body temperature of endothermic species
is regulated by the autonomic mechanisms that control heat production, the distribution of
heat within the body, and the avenues and rate of heat loss from the body to the
environment.
- Other descriptive terms currently used include "temperature conformer" for
ectotherm and "temperature regulator" for endotherm. Some thermal physiologists
prefer a different classification, based on the quality of the thermoregulation: A
homeotherm normally regulates its body temperature within rather narrow limits by varying
its metabolic rate, heat and moisture loss, or position in the environment; a poikilotherm
may allow its body temperature to vary over a considerable range, and regulates that
variation by its position in the environment. Complications for the latter scheme arise
when one considers hibernators (endotherms that periodically become poikilothermic) or
ectotherms that are effectively homeothermic by virtue of efficient behavioral
thermoregulation. The terms "endotherm" and "ectotherm" are used in
the material that follows.
10.2. HEAT EXCHANGE BETWEEN ORGANISM AND
ENVIRONMENT
- Radiofrequency radiation may be regarded conveniently as part of the thermal environment
to which man and other endotherms may be exposed. Figure 10.1 is a schematic
representation of the sources of heat in the body and of the different routes by which
thermal energy may be transferred between the body and the environment. Heat is produced
in the body through metabolic processes (M) and may also be passively generated in body
tissues by absorption of RFR (
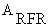 ).
If the body temperature is to remain stable, this thermal energy must be continually
transferred to the environment. As outlined above, the balance between the production and
loss of thermal energy is so regulated by behavioral and autonomic responses that minimal
variation occurs in the body temperature of an endotherm.
).
If the body temperature is to remain stable, this thermal energy must be continually
transferred to the environment. As outlined above, the balance between the production and
loss of thermal energy is so regulated by behavioral and autonomic responses that minimal
variation occurs in the body temperature of an endotherm.
- Energy may be lost (Figure 10.1) by evaporation of water from the respiratory tract (
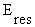 ) or from the skin (
) or from the skin (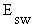 ), by dry-heat transfer from the skin
surface via radiation (
), by dry-heat transfer from the skin
surface via radiation (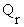 ) or
convection (
) or
convection (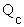 ), and by doing work
(W = force x distance) on the environment. Heat transfer by conduction is usually
insignificant in most species unless they are recumbent. When the environment is thermally
neutral, dry-heat loss predominates in the form of convective transfer to the air and
radiant transfer to the surrounding surfaces. A small amount of heat is always lost by the
diffusion of water through the skin (not shown in the figure).
), and by doing work
(W = force x distance) on the environment. Heat transfer by conduction is usually
insignificant in most species unless they are recumbent. When the environment is thermally
neutral, dry-heat loss predominates in the form of convective transfer to the air and
radiant transfer to the surrounding surfaces. A small amount of heat is always lost by the
diffusion of water through the skin (not shown in the figure).Figure
10.1.
A schematic diagram of the sources of body heat (including radiofrequency radiation) and
the important energy flows between man and the environment. The body is in thermal
equilibrium if the rate of heat loss equals the rate of heat gain. Figure modified from
Berglund (1983)
.
- When the temperature of the environment rises above thermoneutrality, or during vigorous
exercise or defervescence, the evaporation of sweat (
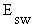 ) dissipates large amounts of body heat. Evaporative water loss
through sweating occurs in man, the great apes, certain other primates, and a few other
species such as horses and camels. Many animals--such as dogs, cats, and rabbits--use
panting (increased respiratory frequency coupled with copious saliva production) to lose
heat by evaporation. Other species, such as the rodents, have no such physiological
mechanisms and must rely on behavioral responses which include seeking shade, burrows, or
aqueous environments and/or grooming their bodies with water, urine, or saliva to aid
evaporative cooling. Table 10.1 includes several thermoregulatory characteristics of
certain animals.
) dissipates large amounts of body heat. Evaporative water loss
through sweating occurs in man, the great apes, certain other primates, and a few other
species such as horses and camels. Many animals--such as dogs, cats, and rabbits--use
panting (increased respiratory frequency coupled with copious saliva production) to lose
heat by evaporation. Other species, such as the rodents, have no such physiological
mechanisms and must rely on behavioral responses which include seeking shade, burrows, or
aqueous environments and/or grooming their bodies with water, urine, or saliva to aid
evaporative cooling. Table 10.1 includes several thermoregulatory characteristics of
certain animals.
- The rate of heat loss from an endotherm is governed by the thermal characteristics of
the environment, as indicated in Figure 10.1; these include not only the air temperature (
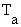 ) but also the air movement (v) and
humidity (RH). Two other environmental variables that affect heat transfer (not shown in
the figure) are the mean radiant temperature of surrounding surfaces , especially those
close to the body, and the amounts of insulation (fur, fat, feathers, clothing).
) but also the air movement (v) and
humidity (RH). Two other environmental variables that affect heat transfer (not shown in
the figure) are the mean radiant temperature of surrounding surfaces , especially those
close to the body, and the amounts of insulation (fur, fat, feathers, clothing).
- When the thermal energy produced in the body (including that derived from absorbed RFR)
is equal to that exchanged with the environment, the body is said to be in thermal
balance. Under these conditions the body temperature remains stable. When heat production
exceeds heat dissipation, thermal energy is stored in the body and the body temperature
rises (hyperthermia). On the other hand, when more heat is transferred to the environment
than can be produced or absorbed, the body temperature falls (hypothermia).
Table 10.1.
Thermoregulatory Characteristics Of Animals
10.3. THE THERMOREGULATORY PROFILE
- The particular thermoregulatory effector response mobilized at any given time, and its
vigor, will depend on the prevailing thermal environment. The ambient temperature is
frequently the only environmental variable specified in research reports, but the
specification of air movement and relative humidity is equally important. Figure 10.2, a
schematic thermoregulatory profile of a typical endotherm, illustrates how the principal
autonomic responses of heat production and heat loss depend on the ambient temperature.
The responses are considered to be steady state rather than transient, and the ambient air
is considered to have minimal movement and water content. Three distinct zones can be
defined in terms of the prevailing autonomic adjustment. Below the lower critical
temperature (LCT), thermoregulation is accomplished by changes in metabolic heat
production, other responses remaining at minimal strength . As the ambient temperature
falls further and further below the LCT, heat production increases proportionately. In a
cool environment RF energy absorbed by an endotherm will spare the metabolic system in
proportion to the field strength and will have no effect on other autonomic responses.
- At ambient temperatures above the LCT, metabolic heat production is at the low resting
level characteristic of the species, evaporative heat loss is minimal, and changes in
thermal conductance accomplish thermoregulation. Conductance is a measure of heat flow
from the body core to the skin and reflects the vasomotor tone of the peripheral
vasculature. As the constricted peripheral vessels begin to dilate, warm blood from the
body core is brought to the surface so that the heat may be lost to the environment by
radiation and convection. These vasomotor adjustments take place within a range of ambient
temperatures, called the thermoneutral zone (TNZ), that is peculiar to each species.
Insofar as they are known, the TNZs for animals commonly used in the laboratory are
indicated in Table 10.1. If an endotherm at thermoneutrality is exposed to RFR, augmented
vasodilation may occur so that the heat generated in deep tissues can be quickly brought
to the skin surface for dissipation to the environment.
- The upper limit of the TNZ is known as the upper critical temperature (UCT). At this
ambient temperature the endotherm is fully vasodilated and
Figure
10.2.
Thermoregulatory profile of a typical endothermic organism to illustrate the dependence of
principal types of autonomic responses on environmental temperature. LCT = lower critical
temperature; UCT = upper critical temperature; TNZ = thermoneutral zone.
dry-heat loss (by convection and radiation) is maximal. Further increases in ambient
temperature provoke the mobilization of heat loss by evaporation, either from the skin
(sweating) or the respiratory tract (panting). Man and certain other mammals have the
ability to sweat copiously to achieve thermoregulation in hot environments. It is
reasonable to assume that if these species were exposed to RFR at ambient temperatures
above the UCT, their sweating rate would increase in proportion to the field strength.
Other mammals, notably the rodents, neither sweat nor pant and when heat stressed must
depend on behavioral maneuvers to achieve some degree of thermoregulation; if the
opportunity for behavioral thermoregulation is curtailed, these animals can rapidly become
hyperthermic when heat stressed. The basic thermoregulatory profile of the selected
laboratory animal must therefore be considered in detail as part of the experimental
design of any research into the biological consequences of exposure to RFR; changes in any
measured thermoregulatory response will depend on the functional relationship between that
response and the prevailing ambient temperature. Other types of responses also may be
indirectly affected by the thermoregulatory profile if they interfere with efficient
thermoregulation (e.g., food and water consumption).
- Man exhibits profound adaptability in the face of environmental thermal stress,
particularly in warm environments. Figure 10.3 illustrates some of the fundamental data
collected by Hardy and DuBois (1941) for nude men and women exposed in a calorimeter to a
wide range of ambient temperature Because of the vigorous responses of heat production and
heat loss, the rectal temperature varies less than 1ºC across a 20ºC range of
calorimeter temperature. The TNZ is extremely narrow, occurring at about 28ºC in the
calorimeter and closer to 30ºC in the natural environment. Above the TNZ, evaporative
heat loss (whole-body sweating) is initiated that can attain rates of 2-3 L/h and up to
10-15 L/d (Wenger, 1983). Assuming normal hydration, it is difficult to increase metabolic
heat production (by exercise) to levels that cannot be dissipated by sweating, unless the
ambient temperature or vapor pressure is very high. Since human evaporative heat loss is
controlled by both peripheral and internal thermal signals (Nadel et al., 1971), only an
extraordinarily hostile thermal environment, which includes a source of RFR, can be
expected to seriously threaten man's thermoregulatory system.
Figure
10.3.
Thermoregulatory profile of nude humans equilibrated in a calorimeter to different ambient
temperatures. Data adapted from Hardy and DuBois (1941).
Way et al. (1981) and others (Stolwijk, 1983) have predicted minimal increases in brain
and body temperatures during local absorption of significant amounts of RF energy, because
of the rapid mobilization of evaporative heat loss and a significant increase in tissue
blood flow. Under the assumption that RF exposure provides a thermal stress comparable to
exercise (Nielsen and Nielsen, 1965) or an ambient temperature well above the TNZ, such
response changes would be predicted from knowledge of the human thermoregulatory profile
in Figure 10.3. On the other hand, significant temperature elevations in certain body
sites (e.g., the legs, arms, and neck) have been predicted by a two-dimensional
heat-transfer model of man exposed to a unilateral planewave at resonant and near-resonant
frequencies (Spiegel et al., 1980). These predictions should be verified in animal models
or, preferably, in human subjects exposed to comparable fields.
10.4. BODY HEAT BALANCE
- The most important principle involved in the study of autonomic thermoregulation of
endotherms is the first law of thermodynamics--the law of conservation of energy (Bligh
and Johnson, 1973). In the steady state the heat produced in the body is balanced by the
heat lost to the environment, so heat storage is minimal. This relationship can be
expressed by a heat-balance equation:
M ± W = R + C + E ± S (Equation
10.1)
in which
- M = rate at which thermal energy is produced through metabolic processes
- W = power, or rate at which work is produced by or on the body
- R = heat exchange with the environment via radiation
- C = heat exchange with the environment via convection
- E = rate of heat loss due to the evaporation of body water
- S = rate of heat storage in the body
- All terms in Equation 10.1 must be in the same units, e.g. , watts (the unit used
throughout this handbook). Physiologists commonly express these quantities in kilocalories
per hour, which can be converted to watts by multiplying by 1.163, the conversion factor.
As Equation 10.1 is written, negative values of R, C, and E may all cause a rise in the
body temperature; positive values may cause a fall. Work (W) is positive when accomplished
by the body (e.g., riding a bicycle), and this potential energy must be subtracted from
metabolic energy (M) to find the net heat (H) developed within the body. When W is
negative (e.g., walking downstairs), this heat is added to M. While W may be a significant
factor for humans or beasts of burden, it may be considered negligible for other
endotherms, particularly in a laboratory setting. Usually evaporative heat loss (E) is
positive; when E is negative, condensation occurs and thermal injury is possible.
- Because heat exchange by radiation, convection, or evaporation is always related in some
way to the surface area of the body, each term in Equation 10.1 is usually expressed in
terms of energy per unit surface area, e.g., watts per square meter. The most commonly
used measure of the body surface area of humans is that proposed by DuBois (1916),
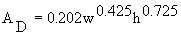 (Equation 10.2)
(Equation 10.2)
where
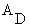 = DuBois surface in square
meters
= DuBois surface in square
meters- w = body mass in kilograms
- h = height in meters
- As noted by Kleiber (1961), h for similar body shapes is proportional to a mean linear
dimension equal to
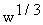 . Therefore,
to compare humans of different sizes, Equation 10.2 may be generalized as
. Therefore,
to compare humans of different sizes, Equation 10.2 may be generalized as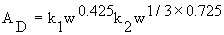 =
=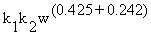 =
=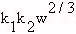 (Equation 10.3)
(Equation 10.3)
- The ratio of surface area to body mass varies between species, so it is difficult to
establish a general rule for the determination of surface area. Many methods have been
devised for the direct measurement of the surface area of experimental animals, most of
which are inaccurate to some degree. In nearly all cases, the surface area is some
function of
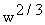 .
.
- Although Equation 10.1 has no term for heat transfer through conduction (which is
usually insignificant under normal conditions), conduction combined with mass transfer
forms the significant mode of heat transfer called convection. Convective heat transfer in
air (C) is a linear function of body surface area (A), and the convective heat transfer
coefficient (
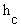 ) is a function of
ambient air motion to the 0.6 power (
) is a function of
ambient air motion to the 0.6 power (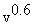 ) The amount of heat the body loses through convection depends on the
difference between the surface temperature of the skin (
) The amount of heat the body loses through convection depends on the
difference between the surface temperature of the skin (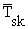 ) and the air temperature, usually taken as the dry-bulb
temperature (
) and the air temperature, usually taken as the dry-bulb
temperature (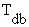 ). The value of the
heat-transfer coefficient depends on certain properties of the surrounding medium, such as
density and viscosity, as well as a shape/dimension factor for the body. Clothing
complicates the analysis and is often evaluated in terms of insulation (clo) units.
). The value of the
heat-transfer coefficient depends on certain properties of the surrounding medium, such as
density and viscosity, as well as a shape/dimension factor for the body. Clothing
complicates the analysis and is often evaluated in terms of insulation (clo) units.
- Heat transfer by radiation is independent of ambient temperature. The wavelengths of the
radiation exchanged between two objects are related to their respective surface
temperatures; the net heat transfer by radiation is proportional to the difference between
their absolute temperatures to the fourth power and to the relative absorptive and
reflective properties of the two surfaces. In general, the net radiant-heat exchange
(where
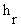 = radiant-heat-transfer
coefficient) between a nude man and the environment involve a estimation of the mean
radiant temperature (MRT). MRT (alternate symbol
= radiant-heat-transfer
coefficient) between a nude man and the environment involve a estimation of the mean
radiant temperature (MRT). MRT (alternate symbol 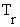 ) can be derived from the temperature (
) can be derived from the temperature (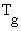 ) of a blackened hollow sphere of thin copper (usually
0.15-m diameter) having heat-transfer characteristics similar to those for the human body
(Woodcock et al., 1960):
) of a blackened hollow sphere of thin copper (usually
0.15-m diameter) having heat-transfer characteristics similar to those for the human body
(Woodcock et al., 1960):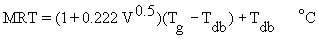 (Equation 10.4)
(Equation 10.4)
Clothing complicates this analysis as it does heat transfer by other modes. Heating by
RFR may further complicate the analysis of radiant-heat exchange between a man and his
environment, although Berglund (1983) has demonstrated that this complex situation can be
analyzed by conventional methods.
- The final avenue of heat loss available to man is that due to the evaporation of water.
The latent heat of vaporization of water at normal body temperature is 0.58 kcal/g; the
body loses this amount of heat when water is evaporated from its surfaces. Water from the
respiratory surfaces is continually being lost in the expired air. Water also continually
diffuses through the skin; this is called insensible water loss or insensible
perspiration. These two avenues contribute equally to a heat loss that totals about 25% of
the resting metabolic heat production of a man in a thermoneutral environment. However,
the major avenue of evaporative heat loss in man is sweating, which depends on the vapor
pressures of the air and the evaporating surface and is thus a direct function of both dry
bulb (
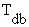 ) and wet bulb (
) and wet bulb (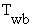 ) temperatures. When
) temperatures. When 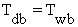 , the air is at 100% relative humidity
and thus no water can be evaporated from the skin surface; at less than 100% relative
humidity, evaporation can occur. The interrelationships between these variables can be
determined from a standard psychrometric chart (ASHRAE Handbook, 1981). In Equation 10.1,
E represents the evaporative cooling allowed by the environment (
, the air is at 100% relative humidity
and thus no water can be evaporated from the skin surface; at less than 100% relative
humidity, evaporation can occur. The interrelationships between these variables can be
determined from a standard psychrometric chart (ASHRAE Handbook, 1981). In Equation 10.1,
E represents the evaporative cooling allowed by the environment (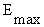 ) and is in no way related to the level of evaporative
cooling required (
) and is in no way related to the level of evaporative
cooling required (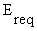 ) by the man.
) by the man.10.5. METABOLIC RATES OF MAN AND ANIMALS
- Because the metabolic heat production per unit body mass, or "Specific metabolic
rate," varies greatly with body size and proportion (somatotype), several measures of
this variable are in wide use. Figure 10.4 is a log-log plot of metabolic heat production
versus body mass for several animals and man. The solid line with a slope of 0.75 reveals
a strong correlation between body mass raised to the 0.75 power and metabolic heat
production. This empirical observation has prompted researchers to adopt power per unit
body mass, in units of watts per kilogram, as the standard metric for animal metabolic
rate.
Figure 10.4.
Logarithm of total metabolic heat production plotted against logarithm of body mass. (Data
taken from Tables 10.2 and 10.4.)
- The metabolic heat production (M) of placental animals (most mammals) can be estimated
by the following formula:
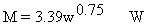 (Equation 10.5)
(Equation 10.5)
where w is the mass of the animal in kilograms. Another useful equation relates the
metabolic heat produced by the body to the rate of oxygen consumption (ASHRAE Handbook,
1981):
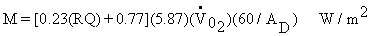 (Equation
10.6)
(Equation
10.6)
where
- RQ = the respiratory quotient, or ratio of
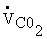 produced to
produced to 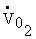 inhaled;
RQ in man may vary from 0.83 (resting ) to over 1.0 ( heavy exercise)
inhaled;
RQ in man may vary from 0.83 (resting ) to over 1.0 ( heavy exercise)
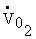 = oxygen consumption in
liters/minute at standard conditions (O°C 760 mmHg)
= oxygen consumption in
liters/minute at standard conditions (O°C 760 mmHg)- 5.87 = the energy equivalent of 1 L of oxygen at standard conditions in watt-hours/liter
when RQ = 1.
Formulas for the metabolic heat production of other classes of animals can
be found in an article by Gordon (1977).
- Another widely accepted form for expressing metabolic heat production is power per unit
surface area. The dashed line in Figure 10.4, with a slope of 0.67, represents how surface
area increases with mass for geometrically similar shapes. This corresponds to the
approximate formula for the body surface area (SA) of these animals:
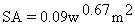 (Equation 10.7)
(Equation 10.7)
Although surface area does not describe the animal data as well as 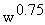 , it is as suitable a measure as any
for human metabolic heat production. For accurate calculations of human metabolic heat
production, the DuBois area (Equation 10.2) should be used.
, it is as suitable a measure as any
for human metabolic heat production. For accurate calculations of human metabolic heat
production, the DuBois area (Equation 10.2) should be used.
- Metabolic heat production (M) is often called "metabolic rate" (MR). Table
10.2 lists resting metabolic rates for normal healthy humans of varying age and
somatotype. The specific metabolic rate (SMR; W/kg) is clearly seen to be a function of
body size and shape.
- The basal metabolic rate (BMR) is defined as the heat production of a human in a
thermoneutral environment (33ºC), at rest mentally and physically and at a time exceeding
12 h from the last meal. The standard BMR for man is about 250 ml
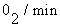 , or 84 W, or 0.8 MET (where 1 MET = 58.2 W/m² ). The
BMR also corresponds to about 1.2 W/kg for a 70-kg "standard" man. The BMR is
altered by changes in active body mass, diet, and endocrine levels but probably not by
living in the heat (Goldman, 1983). In resting man most of the heat is generated in the
core of the body--the trunk, viscera, and brain-despite the fact that these regions
represent only about one-third of the total body mass. This heat is conducted to the other
body tissues, and its elimination from the body is controlled by the peripheral vasomotor
system.
, or 84 W, or 0.8 MET (where 1 MET = 58.2 W/m² ). The
BMR also corresponds to about 1.2 W/kg for a 70-kg "standard" man. The BMR is
altered by changes in active body mass, diet, and endocrine levels but probably not by
living in the heat (Goldman, 1983). In resting man most of the heat is generated in the
core of the body--the trunk, viscera, and brain-despite the fact that these regions
represent only about one-third of the total body mass. This heat is conducted to the other
body tissues, and its elimination from the body is controlled by the peripheral vasomotor
system.
- Table 10.3 shows the wide variation of metabolic rates during various activities. All of
these data are given for a healthy normal 20- to 24-yr-old male except as noted. The range
of metabolic rate for humans--considering work performed and assorted physiological
variables such as age, sex, and size--is roughly 40 to 800 W/m² (1 to 21 W/kg for
"standard" man), depending on physical fitness and level of activity. The
influence of age and sex on the metabolic rate of humans is shown in Figures 10.5 and
10.6. Other factors that may influence the metabolic rate are endocrine state, diet, race,
pregnancy, time of day, and emotional state. If deep-body temperature is altered, from
either heat storage in warm environments or febrile disease, a comparable change occurs in
the metabolic rate (Stitt et al., 1974). Similar changes occur when deep-body temperature
rises during exposure to RFR (Adair and Adams, 1982).
Table 10.2.
Resting Metabolic Rates For Normal Healthy Humans Of Specific Age and Somatotype (adapted
from Ruch and Patton, 1973)
Table 10.3.
Variation of Metabolic Rate with Activity For a Normal 20-24-Year-Old Male* (adapted from
Ruch and Patton, 1973)
Figure 10.5.
Variation of human resting metabolic rate (RMR), with age and sex, expressed as power per
unit surface area. Data from Ruch and Patton (1973).
Figure 10.6.
Variation of human resting metabolic rate (RMR), with age and sex, expressed as power per
unit body mass. Data from Figure 10.5 converted by means of average height and weight in
Dreyfuss (1967).
- Resting metabolic rates (MR) for some adult laboratory animals are shown in Table 10.4
in three different forms: total MR for the weight given, specific MR, and standardized MR.
Table 10.4.
Resting Metabolic Rates For Adult Laboratory Animals
A rough idea of metabolic heat production can be gained from an animal's oxygen
consumption (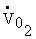 ) by using the
formula
) by using the
formula
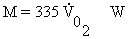 (Equation
10.8)
(Equation
10.8)
where 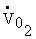 = liters of oxygen
consumed per minute. The energy equivalent of oxygen is approximately 4.8 kcal/L
= liters of oxygen
consumed per minute. The energy equivalent of oxygen is approximately 4.8 kcal/L 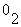 for a typical animal diet, and the
respiratory quotient (RQ) is approximately 0.85.
for a typical animal diet, and the
respiratory quotient (RQ) is approximately 0.85.
10.6. AVENUES OF HEAT LOSS
- Changes in vasomotor tonus and evaporation of body water through active sweating (or
panting in certain endotherms) are both mechanisms of body heat loss. As detailed in
Section 10.3 (Figures 10.2 and 10.3), vasomotor control normally operates to regulate the
body temperature when an endotherm is in a thermoneutral environment, i.e., within the
TNZ. Sweating (or panting) is activated in warmer environments and during exercise and
defervescence.
10.6.1. Vasomotor Control
- Convective heat transfer via the circulatory system is controlled by the sympathetic
nervous system. Below the LCT, vasoconstriction of the peripheral vasculature in arm, leg,
and trunk skin minimizes heat loss from the skin, leaving a residual conductive heat flow
of 5-9 W/m per ºC difference between body core and skin. For a body in the TNZ, when the
peripheral vessels are vasodilated, each liter of blood at 37ºC that flows to the skin
and returns 1ºC cooler allows the body to lose about 1 kcal, or 1.16 W•h, of heat
(Hardy, 1978). During vigorous exercise in the heat, peripheral blood flow can increase
almost tenfold; this increase is essential to eliminate the increased metabolic heat
produced in the working muscles.
- Tissue conductance (K) represents the combined effect of two channels of heat transfer
in the body--conductive heat transfer through layers of muscle and fat and convective heat
transfer by the blood. Tissue thermal conductance is defined as the rate of heat transfer
per unit area during a steady state when a difference of 1ºC is maintained across a layer
of tissue (W/m² • ºC) Johnson, 1973. Although K cannot be measured directly in the
human organism, it can be estimated for resting humans under the assumption that all the
heat is produced in the core of the body and is transferred to the skin and thence to the
environment. Thus
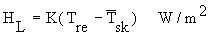 (Equation 10.9)
(Equation 10.9)
in which 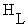 represents the heat
loss (neglecting that lost through respiretion), Tre is rectal or core
temperature, and
represents the heat
loss (neglecting that lost through respiretion), Tre is rectal or core
temperature, and 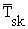 is the average
skin temperature. In the cold (22-28ºC), conductance is minimal for both men and women,
ranging between 6 and 9 W/m² • ºC. In warm environments conductance increases
rapidly, and women show a faster increase than men (Cunningham, 1970; also see Figure
10.3).
is the average
skin temperature. In the cold (22-28ºC), conductance is minimal for both men and women,
ranging between 6 and 9 W/m² • ºC. In warm environments conductance increases
rapidly, and women show a faster increase than men (Cunningham, 1970; also see Figure
10.3).
- Evaporation of sweat from the skin surface efficiently removes heat even in environments
warmer than the skin. In this case, evaporative heat loss must take care of both metabolic
heat and that absorbed from the environment by radiation and convection. We have no reason
to believe that thermalizing energy from absorbed RFR will be dealt with any differently
than heat produced by normal metabolic processes or absorbed by exposure to warm
environments.
- Normal secretory functioning of the approximately 2.5 million sweat glands on the skin
of a human being is essential to the prevention of dangerous hyperthermia. Secretion is
controlled by the sympathetic nervous system and occurs when the ambient temperature rises
above 30-31ºC or the body temperature rises above 37ºC. Local sweating rate also depends
on the local skin temperature (Nadel et al., 1971). Physically fit individuals and those
acclimated to warm environments sweat more efficiently and at a lower internal body
temperature than normal (Nadel et al., 1974). Dehydration or increased salt intake will
alter plasma volume and decrease sweating efficiency (Greenleaf, 1973).
- The maximum sweat rate for humans and the length of time it can be maintained are
limited. The maximum rate of sweat production by an average man is about 30 g/min. If the
ambient air movement and humidity are low enough for all this sweat to be evaporated, the
maximum cooling will be about 675 W/m²; however, conditions are not usually this
ideal--some sweat may roll off the skin or be absorbed by layers of clothing. A more
practical limit of cooling is 350 W/m², or 6 METS, which represents about 17 g/min for
the average man (ASHRAE Handbook, 1981).
10.7. HEAT-RESPONSE
CALCUIATIONS
10.7.1. Models of the Thermoregulatory System
- The operating characteristics of the thermoregulatory system appear to be similar to
those of an automatic control system involving negative feedback. The body temperature of
endotherms appears to be regulated at a set, or reference, level. Temperature sensors
located in the skin and various other parts of the body detect temperature perturbations
and transmit this information to a central integrator,or controller, that integrates the
sensory information, compares the integrated signal with the set point, and generates an
output command to the effector systems for heat production or loss. The responses thus
mobilized tend to return the body temperature back to the set level.
- These hypothetical constructs aid our understanding of thermoregulatory processes and
let us formulate simulation models that can be used to predict human response to a wide
variety of thermal stressors. Models have been of many types, from verbal descriptions to
highly sophisticated electrical analogs and mathematical models. Hardy (1972) gives a
comprehensive account of the development of modeling in thermal physiology. Many
simulation models have been used to predict human responses to RFR (Farr et al., 1971). Of
particular relevance are the theoretical models of Mumford (1969) and Guy et al. (1973)
that use a heat-stress index to describe man's response to particular environmental and RF
heat loads. A model by Emery et al. (1976b) uses several sweat rates to calculate the
thermal response of the body to absorbed RFR. A model of Stolwijk and Hardy (1966) has
been combined with simulations of RFR energy deposition by Stolwijk (1980) and Way et al.
(1981) to demonstrate that the rise in local temperatures in the human body, especially in
the brain, may be much less than anticipated during the localized deposition of RF energy,
even when the radiation is focused on the hypothalamus. Greatly enhanced evaporative heat
loss, skin blood flow, and conductance serve to protect individual body tissues during RFR
energy deposition. On the other hand, a two-dimensional, combined RF-heat-transfer model
developed by Spiegel et al. (1980) predicts rapid localized temperature increments in the
thigh of a nude male resting at thermoneutrality and exposed to 80 MHz at 50 mW/cm², and
similar temperature increments in the steady state at power densities as low as 10
mW/cm². Adding to this model the altered tissue blood flow for temperatures in excess of
40ºC may modify these predictions.
10.7.2. Data for Heat-Response
Calculations
- Much is known about the upper limits of human tolerance to hot, humid environments that
contain no source of RFR (Givoni and Goldman, 1972; Proving et al., 1962). Knowing what
the human tolerance time would be for a given SAR would be useful. This section describes
calculations of the approximate SAR that will produce a critical internal body temperature
in a standard man exposed for 60 min in a specified hot and humid environment.
- The body's two physiological mechanisms that deal with heat stress, vasomotor and
sudomotor, are each a complex function of many variables. The problem can be simplified,
however, if we assume that the body is calling upon its maximum thermoregulatory capacity.
Under most conditions of severe thermal stress, evaporative cooling is limited by the
evaporation rate, not the sweat rate since the maximum sweat rate is over 2 L/h. If the
psychrometric conditions (air temperature, relative humidity, and air velocity), skin
temperature, and clothing characteristics are known, the heat storage in the body can be
calculated by the fundamental heat-balance equation (10.1).
- Agreement is not complete on the physiological criteria that best describe the limits of
human thermal tolerance. Several researchers (Ellis et al., 1964; Craig et al., 1954;
Goldman et al., 1965; Wyndham et al., 1965) have used a rectal temperature (
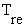 ) of 39.2ºC as a useful criterion for
setting the upper level of heat-stress tolerance in clinical trials. Others have advocated
the use of more subjective criteria such as faintness and loss of mental and physical
ability (Bell and Walters, 1969; Bell et al., 1965; Machle and Hatch, 1947). Since
quantitative calculations based on such subjective criteria are not practical, for the
purposes of the following calculations we have defined a
) of 39.2ºC as a useful criterion for
setting the upper level of heat-stress tolerance in clinical trials. Others have advocated
the use of more subjective criteria such as faintness and loss of mental and physical
ability (Bell and Walters, 1969; Bell et al., 1965; Machle and Hatch, 1947). Since
quantitative calculations based on such subjective criteria are not practical, for the
purposes of the following calculations we have defined a 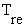 of 39.2ºC as the danger level for man. With this definition, the
critical rate of heating for a 1-h period is that which will cause a rise in
of 39.2ºC as the danger level for man. With this definition, the
critical rate of heating for a 1-h period is that which will cause a rise in 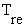 of 2.2ºC/h, assuming a normal
beginning rectal temperature of 37ºC and neglecting any temporal lag in the
of 2.2ºC/h, assuming a normal
beginning rectal temperature of 37ºC and neglecting any temporal lag in the 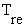 response.
response.
- We utilized data for the change in mean skin temperature (
 ) as a function of time collected in an experiment
recorded by Ellis et al. (1964), in which a healthy 28-yr-old male exposed to a hot, humid
environment was judged by observers to have reached his tolerance limit in 61 min. His
final rectal temperature was 39.4ºC. His skin temperature rose bimodally from 36.9 to
38.4ºC during the first 20 min of exposure, then increased more slowly to 39.3ºC in the
next 41 min because of the onset of sweating.
) as a function of time collected in an experiment
recorded by Ellis et al. (1964), in which a healthy 28-yr-old male exposed to a hot, humid
environment was judged by observers to have reached his tolerance limit in 61 min. His
final rectal temperature was 39.4ºC. His skin temperature rose bimodally from 36.9 to
38.4ºC during the first 20 min of exposure, then increased more slowly to 39.3ºC in the
next 41 min because of the onset of sweating.
- If these data for
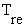 and
and  are assumed to be generally true for
a man heat stressed to his tolerance point in 1 h, we should be able to calculate lesser
amounts of heat storage imposed on the body by less severe environmental conditions that
permit greater rates of evaporative cooling. Also, substituting an equivalent amount of
heat energy absorbed during exposure to RFR for metabolic energy seems reasonable. Such an
equivalence was demonstrated by Nielsen and Nielsen (1965) when they measured identical
thermoregulatory responses to exercise and to diathermic heating. This assumption would be
expected to be valid for RFR at frequencies up to the postresonance region (perhaps up to
about 1 GHz for the average man), but might not be valid at higher frequencies where the
RFR causes primarily surface heating. Consequently, the results calculated in the next
section are restricted to radiation conditions where the RF heating does not occur
primarily on the surface. The substituted equivalent RFR heat load, expressed in watts per
kilogram of body mass, is designated the
are assumed to be generally true for
a man heat stressed to his tolerance point in 1 h, we should be able to calculate lesser
amounts of heat storage imposed on the body by less severe environmental conditions that
permit greater rates of evaporative cooling. Also, substituting an equivalent amount of
heat energy absorbed during exposure to RFR for metabolic energy seems reasonable. Such an
equivalence was demonstrated by Nielsen and Nielsen (1965) when they measured identical
thermoregulatory responses to exercise and to diathermic heating. This assumption would be
expected to be valid for RFR at frequencies up to the postresonance region (perhaps up to
about 1 GHz for the average man), but might not be valid at higher frequencies where the
RFR causes primarily surface heating. Consequently, the results calculated in the next
section are restricted to radiation conditions where the RF heating does not occur
primarily on the surface. The substituted equivalent RFR heat load, expressed in watts per
kilogram of body mass, is designated the 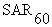 --the specific absorption rate that would produce a rectal temperature of
39.2ºC in the irradiated subject in 60 min. The
--the specific absorption rate that would produce a rectal temperature of
39.2ºC in the irradiated subject in 60 min. The 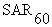 is intended to represent the maximum SAR that a healthy average
man can tolerate, with regard to thermal considerations alone, for 60 min in a given
environment, assuming both that the capacity to thermoregulate is normal and that the
other criteria for metabolic rate, posture, clothing, and behavior specified below are
valid.
is intended to represent the maximum SAR that a healthy average
man can tolerate, with regard to thermal considerations alone, for 60 min in a given
environment, assuming both that the capacity to thermoregulate is normal and that the
other criteria for metabolic rate, posture, clothing, and behavior specified below are
valid.
- For the following calculations the required parameters for man and the environment are
listed in Table 10.5. Standard values obtained from physiology texts (Kerslake, 1972;
Mountcastle, 1974; Newburgh, 1949; Ruch and Patton, 1973) are given for the sample
calculations. The symbols, units, and conversion factors used in this section conform for
the most part to the uniform standards proposed by Gagge et al. (1969).
- The calculations are based on a modification of the fundamental heatbalance equation
(10.1) which neglects the work factor (W), groups together the terms for dry-heat losses
(R + C), and incorporates the electromagnetic power absorbed (P):
M + P =
(R + C) + E + S
or
S = M - (R + C) - E + P (Equation 10.10)
in which all symbols are as previously defined. The total heat load is given
by
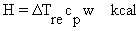 (Equation
10.11)
(Equation
10.11)
where 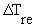 is the change in rectal
temperature caused by heat load H. The evaporation rate is given by
is the change in rectal
temperature caused by heat load H. The evaporation rate is given by
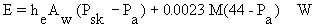 (Equation
10.12)
(Equation
10.12)
The dry-heat losses due to radiation and convection can be represented by
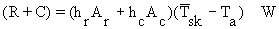 (Equation
10.13)
(Equation
10.13)
Table 10.5.
Specification Of Parameters Used In Calculating 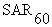
Combining Equations 10.10, 10.12, and 10.13 and using values from Table 10.5 results in
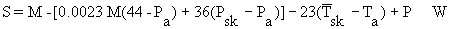 (Equation
10.14)
(Equation
10.14)
This equation is first solved for the particular psychrometric conditions of interest
with no RF power absorbed (P = 0). Over a 1-h period, the heat load due to the environment
alone is given by
 (Equation
10.15)
(Equation
10.15)
The solution is -60 kcal when 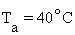 and
and 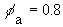 . By Equation 10.11, the heat
load that causes a 2.2ºC rise in
. By Equation 10.11, the heat
load that causes a 2.2ºC rise in 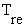 was 128 kcal for this particular man.
was 128 kcal for this particular man.
The power, P, that will cause a 2.2ºC rise in 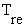 in 1 h is the difference between H and 128 kcal.
in 1 h is the difference between H and 128 kcal.
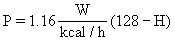
P = 218 W
The 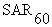 is simply
is simply
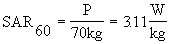
By using the SAR curves for an average man, we can plot the incident power density that
will produce the 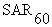 for any given
frequency and polarization, as shown in Figure 10.7. The calculated
for any given
frequency and polarization, as shown in Figure 10.7. The calculated 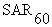 values plotted on this graph represent the worst
possible case for man, which is, according to the data for the prolate spheroidal model, E
polarization at resonance (70 MHz).
values plotted on this graph represent the worst
possible case for man, which is, according to the data for the prolate spheroidal model, E
polarization at resonance (70 MHz).
- In Figure 10.7 the intercept of each curve with the horizontal axis indicates the
ambient conditions (temperature and relative humidity) that will produce a rectal
temperature of 39.2ºC with no irradiation. For example, with a relative humidity of 80%
and an ambient temperature of 42ºC, the
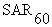 is zero--which means that under these conditions a rectal temperature of
39.2ºC will occur in 1 h with no irradiation. Similarly, the curve shows that if the
ambient temperature were 41ºC and the relative humidity 80%, the
is zero--which means that under these conditions a rectal temperature of
39.2ºC will occur in 1 h with no irradiation. Similarly, the curve shows that if the
ambient temperature were 41ºC and the relative humidity 80%, the 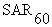 would be 1.25 W/kg--under these conditions a rectal
temperature of 39.2ºC would be reached in 60 min. The other curves in the figure indicate
that the same SAR (1.25 W/kg) would occur at 49ºC and 50% relative humidity and at 63ºC
and 20% relative humidity. From the ordinate on the right, we read that at this
would be 1.25 W/kg--under these conditions a rectal
temperature of 39.2ºC would be reached in 60 min. The other curves in the figure indicate
that the same SAR (1.25 W/kg) would occur at 49ºC and 50% relative humidity and at 63ºC
and 20% relative humidity. From the ordinate on the right, we read that at this 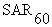 , the incident power density for E
polarization at resonance would be 5 mW/cm². The incident power densities at other
frequencies and/or polarizations can be determined by using the dosimetric curves to find
what power density produces an SAR of 1.25 W/kg for the given frequency and polarization
in question.
, the incident power density for E
polarization at resonance would be 5 mW/cm². The incident power densities at other
frequencies and/or polarizations can be determined by using the dosimetric curves to find
what power density produces an SAR of 1.25 W/kg for the given frequency and polarization
in question.Figure 10.7.
Calculated 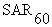 values in an average
man, unclothed and quiet, irradiated by an electromagnetic planewave with E polarization
at resonance (about 70 MHz). Dashed horizontal lines indicate the psychrometric conditions
(in still air) that yield an
values in an average
man, unclothed and quiet, irradiated by an electromagnetic planewave with E polarization
at resonance (about 70 MHz). Dashed horizontal lines indicate the psychrometric conditions
(in still air) that yield an 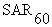 of
1.25 W/kg and 0.4 W/kg at this frequency.
of
1.25 W/kg and 0.4 W/kg at this frequency.
- If the ambient temperature were 41ºC and the relative humidity only 20%, a very high
SAR would be required to produce a rectal temperature of 39.2ºC in 60 min, a value too
high to be read from Figure 10.7. This shows that, as expected, in warm environments the
relative humidity has a great effect on the body's ability to dissipate an added thermal
burden by evaporation. We strongly emphasize that the
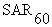 is only an estimate of the upper limit of thermal tolerance for a
healthy nude man. Many other factors must be considered, not the least of which is the
great disparity in thermoregulatory response from individual to individual.
is only an estimate of the upper limit of thermal tolerance for a
healthy nude man. Many other factors must be considered, not the least of which is the
great disparity in thermoregulatory response from individual to individual.
- Figure 10.7 shows the relative independence of the
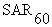 on the prevailing ambient temperature at any given ambient
humidity level. Thus at such moderate SARs, hyperthermic levels of body temperature can be
expected only if the body is already operating at near-critical environmental conditions.
Under such hostile conditions even small increases in metabolic heat production, such as
very light work, will also initiate an increase in the body temperature. The basis for RF
exposure guidelines currently in force, 0.4 W/kg, is also indicated on the curves in
Figure 10.7 under the assumption of a 60-min average time. (The 6-min averaging time
specified in the current guidelines is far too short to achieve a thermal steady state
such as that represented in Figure 10.7.) The reduction in ambient temperature required,
at any relative humidity, to accommodate an
on the prevailing ambient temperature at any given ambient
humidity level. Thus at such moderate SARs, hyperthermic levels of body temperature can be
expected only if the body is already operating at near-critical environmental conditions.
Under such hostile conditions even small increases in metabolic heat production, such as
very light work, will also initiate an increase in the body temperature. The basis for RF
exposure guidelines currently in force, 0.4 W/kg, is also indicated on the curves in
Figure 10.7 under the assumption of a 60-min average time. (The 6-min averaging time
specified in the current guidelines is far too short to achieve a thermal steady state
such as that represented in Figure 10.7.) The reduction in ambient temperature required,
at any relative humidity, to accommodate an 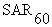 of 0.4 W/kg is less than can be precisely achieved or measured, given present
technology; therefore, no temperature or humidity factors should be used to adjust
0.4-W/kg RF exposures.
of 0.4 W/kg is less than can be precisely achieved or measured, given present
technology; therefore, no temperature or humidity factors should be used to adjust
0.4-W/kg RF exposures.
- A healthy person exposed to the environments represented in the SAR curves would be
expected to experience considerable thermal discomfort along with the rise in core
temperature, rise in heart rate, and profuse sweating. All of these responses would
increase over time until, at about 60 min, the person would be on the verge of collapse
and exhibiting the unpleasant but reversible symptoms reported in experiments on human
heat tolerance.
- Because of the approximations used in the calculations described here and the great
differences in thermoregulatory response found from person to person, we emphasize that
the calculated data given in this handbook are intended to serve only as guidelines and to
give a qualitative indication of anticipated responses.

Go to Chapter 11.
Return to Table of Contents.
Last modified: June 14, 1997
© October 1986, USAF School of Aerospace Medicine, Aerospace Medical Division (AFSC),
Brooks Air Force Base, TX 78235-5301


![]()
![]() (Equation 10.2)
(Equation 10.2) 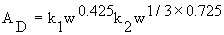 =
=![]() =
=![]() (Equation 10.3)
(Equation 10.3) ![]() (Equation 10.4)
(Equation 10.4) ![]() (Equation 10.5)
(Equation 10.5) ![]() (Equation
10.6)
(Equation
10.6) ![]() (Equation 10.7)
(Equation 10.7) ![]() , it is as suitable a measure as any
for human metabolic heat production. For accurate calculations of human metabolic heat
production, the DuBois area (Equation 10.2) should be used.
, it is as suitable a measure as any
for human metabolic heat production. For accurate calculations of human metabolic heat
production, the DuBois area (Equation 10.2) should be used.![]() ) by using the
formula
) by using the
formula![]() (Equation
10.8)
(Equation
10.8) ![]() = liters of oxygen
consumed per minute. The energy equivalent of oxygen is approximately 4.8 kcal/L
= liters of oxygen
consumed per minute. The energy equivalent of oxygen is approximately 4.8 kcal/L ![]() for a typical animal diet, and the
respiratory quotient (RQ) is approximately 0.85.
for a typical animal diet, and the
respiratory quotient (RQ) is approximately 0.85.![]() (Equation 10.9)
(Equation 10.9) ![]() represents the heat
loss (neglecting that lost through respiretion), Tre is rectal or core
temperature, and
represents the heat
loss (neglecting that lost through respiretion), Tre is rectal or core
temperature, and ![]() is the average
skin temperature. In the cold (22-28ºC), conductance is minimal for both men and women,
ranging between 6 and 9 W/m² • ºC. In warm environments conductance increases
rapidly, and women show a faster increase than men (Cunningham, 1970; also see Figure
10.3).
is the average
skin temperature. In the cold (22-28ºC), conductance is minimal for both men and women,
ranging between 6 and 9 W/m² • ºC. In warm environments conductance increases
rapidly, and women show a faster increase than men (Cunningham, 1970; also see Figure
10.3).![]() (Equation
10.11)
(Equation
10.11) ![]() is the change in rectal
temperature caused by heat load H. The evaporation rate is given by
is the change in rectal
temperature caused by heat load H. The evaporation rate is given by![]() (Equation
10.12)
(Equation
10.12) ![]() (Equation
10.13)
(Equation
10.13) ![]() (Equation
10.14)
(Equation
10.14) 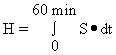 (Equation
10.15)
(Equation
10.15) ![]() and
and ![]() . By Equation 10.11, the heat
load that causes a 2.2ºC rise in
. By Equation 10.11, the heat
load that causes a 2.2ºC rise in ![]() was 128 kcal for this particular man.
was 128 kcal for this particular man.![]() in 1 h is the difference between H and 128 kcal.
in 1 h is the difference between H and 128 kcal.![]()
![]() is simply
is simply![]()
![]() for any given
frequency and polarization, as shown in Figure 10.7. The calculated
for any given
frequency and polarization, as shown in Figure 10.7. The calculated ![]() values plotted on this graph represent the worst
possible case for man, which is, according to the data for the prolate spheroidal model, E
polarization at resonance (70 MHz).
values plotted on this graph represent the worst
possible case for man, which is, according to the data for the prolate spheroidal model, E
polarization at resonance (70 MHz).![]()